



Next: Memory Constraints
Up: Theory: Optimization Methods
Previous: Quasi-Newton (Variable Metric)
If we are able to efficiently calculate both the gradient,
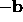 , and the Hessian matrix, A, at a given point
a then we can use more efficient algorithms for locating
the minima. In the above an iterative solution was required both
because we were dealing with non-linear functions and in order to
build up an estimate of the Hessian (either directly or indirectly).
If we have a twice-differentiable analytic form for the function
, and the Hessian matrix, A, at a given point
a then we can use more efficient algorithms for locating
the minima. In the above an iterative solution was required both
because we were dealing with non-linear functions and in order to
build up an estimate of the Hessian (either directly or indirectly).
If we have a twice-differentiable analytic form for the function
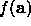 we can generate the Hessian directly.
The Levenberg-Marquardt (LM) Method uses a neat trick to take
advantage of this.
We saw above that if A is a good approximation to the
actual form at the minimum (this is usually close to the true minimum) then
we should update our current estimate of the minimum, a,
using
we can generate the Hessian directly.
The Levenberg-Marquardt (LM) Method uses a neat trick to take
advantage of this.
We saw above that if A is a good approximation to the
actual form at the minimum (this is usually close to the true minimum) then
we should update our current estimate of the minimum, a,
using

However, if we are too far from the minimum A may not be
a good approximation to the local shape of the function, and the
best we can do is to move in a downhill direction

The LM algorithm combines these approaches in the following way:
Define a new n x n matrix 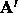 from A as follows
from A as follows
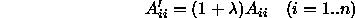

Where 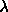 is a regularization constant. At any point, a, the suggested next point is given by
is a regularization constant. At any point, a, the suggested next point is given by
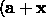 ) where x is the solution to
) where x is the solution to
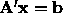 .
When
.
When 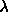 is small
is small 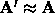 , so we get a Newton-type jump toward the minima. When
, so we get a Newton-type jump toward the minima. When 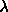 is large
is large
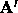 becomes diagonally dominant and x gives a guess at a
suitable downhill step.
becomes diagonally dominant and x gives a guess at a
suitable downhill step.
We start with a modest value for 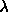 , say 0.001, and evaluate
, say 0.001, and evaluate 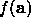 .
The algorithm then proceeds as follows:
.
The algorithm then proceeds as follows:
- Solve for x and evaluate
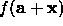
- If
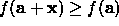 increase
increase 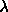 by a factor of 10.
by a factor of 10.
- If
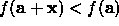 decrease
decrease 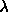 by a factor of 10 and update the current solution
by a factor of 10 and update the current solution 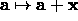
The algorithm iterates until some convergence criteria are reached. Typically
this means that we stop when successive improvements in the value of 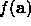 only change its value by some small fraction ( for instance
only change its value by some small fraction ( for instance 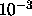 ).
).




Next: Memory Constraints
Up: Theory: Optimization Methods
Previous: Quasi-Newton (Variable Metric)
Bob Fisher
Fri Mar 28 14:12:50 GMT 1997
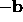 , and the Hessian matrix, A, at a given point
a then we can use more efficient algorithms for locating
the minima. In the above an iterative solution was required both
because we were dealing with non-linear functions and in order to
build up an estimate of the Hessian (either directly or indirectly).
If we have a twice-differentiable analytic form for the function
, and the Hessian matrix, A, at a given point
a then we can use more efficient algorithms for locating
the minima. In the above an iterative solution was required both
because we were dealing with non-linear functions and in order to
build up an estimate of the Hessian (either directly or indirectly).
If we have a twice-differentiable analytic form for the function
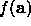 we can generate the Hessian directly.
The Levenberg-Marquardt (LM) Method uses a neat trick to take
advantage of this.
We saw above that if A is a good approximation to the
actual form at the minimum (this is usually close to the true minimum) then
we should update our current estimate of the minimum, a,
using
we can generate the Hessian directly.
The Levenberg-Marquardt (LM) Method uses a neat trick to take
advantage of this.
We saw above that if A is a good approximation to the
actual form at the minimum (this is usually close to the true minimum) then
we should update our current estimate of the minimum, a,
using






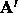 from A as follows
from A as follows
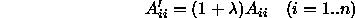

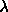 is a regularization constant. At any point, a, the suggested next point is given by
is a regularization constant. At any point, a, the suggested next point is given by
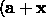 ) where x is the solution to
) where x is the solution to
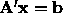 .
When
.
When 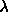 is small
is small 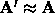 , so we get a Newton-type jump toward the minima. When
, so we get a Newton-type jump toward the minima. When 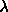 is large
is large
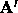 becomes diagonally dominant and x gives a guess at a
suitable downhill step.
becomes diagonally dominant and x gives a guess at a
suitable downhill step.
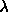 , say 0.001, and evaluate
, say 0.001, and evaluate 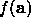 .
The algorithm then proceeds as follows:
.
The algorithm then proceeds as follows:
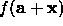
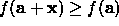 increase
increase 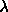 by a factor of 10.
by a factor of 10.
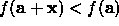 decrease
decrease 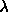 by a factor of 10 and update the current solution
by a factor of 10 and update the current solution 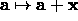
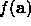 only change its value by some small fraction ( for instance
only change its value by some small fraction ( for instance 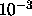 ).
).