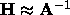Quasi-Newton methods attempt to generate an estimate of the inverse
of the Hessian matrix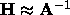 
. This
is then used to determine the next iteration point.
The gradient in the region around a is given by
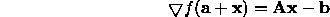
At the minima the gradient is zero
thus the best next direction step is given by
The BFGS (`Broyden-Fletcher-Goldfarb-Shanno') algorithm is based on this technique [6].