



Next: Quasi-Newton (Variable Metric)
Up: Theory: Optimization Methods
Previous: Conjugate Directions
Suppose that we can efficiently calculate the gradient vector
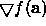 at a point (by `efficiently' we mean
analytically, requiring less computation than n individual evaluations
of the original function). There are cunning `Conjugate Gradient' algorithms available which
use this information to build up conjugate sets much faster than Powell's
method (n line minimizations rather than
at a point (by `efficiently' we mean
analytically, requiring less computation than n individual evaluations
of the original function). There are cunning `Conjugate Gradient' algorithms available which
use this information to build up conjugate sets much faster than Powell's
method (n line minimizations rather than 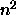 ). See [6].
). See [6].
Bob Fisher
Fri Mar 28 14:12:50 GMT 1997
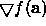 at a point (by `efficiently' we mean
analytically, requiring less computation than n individual evaluations
of the original function). There are cunning `Conjugate Gradient' algorithms available which
use this information to build up conjugate sets much faster than Powell's
method (n line minimizations rather than
at a point (by `efficiently' we mean
analytically, requiring less computation than n individual evaluations
of the original function). There are cunning `Conjugate Gradient' algorithms available which
use this information to build up conjugate sets much faster than Powell's
method (n line minimizations rather than 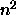 ). See [6].
). See [6].



