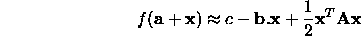
Having performed a line minimization along a direction u we would like to choose a new direction v so that minimizing along v will not `spoil' the minimization along u. We can determine such a direction by using the Taylor approximation at a
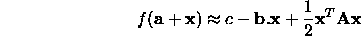
The gradient of f near a is given by
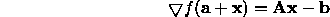
If we have just minimized along a direction u then the component of the gradient along u must be zero, thus the gradient itself is perpendicular to u
As we now move along some direction v the gradient changes by
In order not to interfere with our u minimization we require that the gradient remain perpendicular to u, ie that the change in gradient itself be perpendicular to u. This is simply
Two vectors, u, v, having this property are said to be conjugate. A set of vectors for which this holds for all pairs is a conjugate set.
If we minimize along each of a conjugate set of n directions we will get closer to the minimum efficiently. If the function has an exact quadratic form, one pass through the set will get us exactly to the minimum. Otherwise we must repeat the cycle a number of times.
The problem is, how do we generate such a conjugate set? If f is second-differentiable we can calculate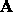 
and generate the
set using algebraic techniques. However, there are much more effective
methods available in such cases (see below). If no derivatives are
available a method due to Powell can be used which generates a conjugate set
a sequence of line minimizations. It starts by assuming
a set consisting of the unit directions, then gradually calculates new
directions from the results of the search. Each n line minimizations
gives an extra conjugate direction, so a full set is derived after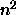 
line minimizations. Details are given in [6].
Powell's is the method of choice if we have a reasonable starting approximation, we cannot easily obtain derivatives and the function isn't too noisy.