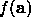 . We can refine this by choosing some direction vector u and
searching for the minimum along the line
. We can refine this by choosing some direction vector u and
searching for the minimum along the line 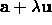 .
This is a 1-D minimization to find the value of
.
This is a 1-D minimization to find the value of  which minimizes the
function
which minimizes the
function  . a is then replaced
with
. a is then replaced
with 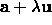 .
.




Suppose we have an estimate a of the minimum of
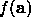 . We can refine this by choosing some direction vector u and
searching for the minimum along the line
. We can refine this by choosing some direction vector u and
searching for the minimum along the line 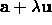 .
This is a 1-D minimization to find the value of
.
This is a 1-D minimization to find the value of  which minimizes the
function
which minimizes the
function  . a is then replaced
with
. a is then replaced
with 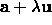 .
.
The simplest algorithm for locating the minima of 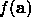 is to repeat this
process, cycling through the n unit direction vectors which span the
parameter space. However, this can prove to be very inefficient if we
end up making many small steps, zig-zagging along a valley, when it would
be better to move in directions aligned with the valley (Figure 3).
is to repeat this
process, cycling through the n unit direction vectors which span the
parameter space. However, this can prove to be very inefficient if we
end up making many small steps, zig-zagging along a valley, when it would
be better to move in directions aligned with the valley (Figure 3).

Figure 3: Minimizing along each unit direction in turn can be inefficient.