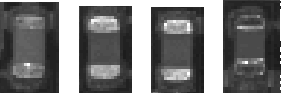
Figure 5: Surface mount components can vary significantly in appearance




Suppose we wish to locate an object whose shape is fixed, but whose grey-level appearance can vary. For instance, surface mount components on printed circuit boards usually have a fixed size, but their appearance can vary due to differences in printing across batches and manufacturers and the variations in local lighting conditions(Figure 5). Attempting to locate such components with standard correllation methods can fail because of this variation.
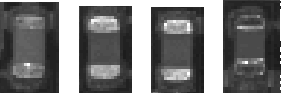
Figure 5: Surface mount components can vary significantly in appearance
A better approach is to build a statistical
model of the variation. We represent the component as a rectangle of
the n pixels with values 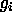 which we concatenate into a vector g.
We then take a training set of examples of the component, each with
different appearance vectors g, and estimate the mean
which we concatenate into a vector g.
We then take a training set of examples of the component, each with
different appearance vectors g, and estimate the mean  and the covariance matrix S. We would
like to test how well a patch,
and the covariance matrix S. We would
like to test how well a patch, 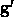 , sampled from an image at
a position
, sampled from an image at
a position  and at orientation
and at orientation 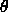 , matches the examples seen
in the training set. If we make the
(perhaps rash) assumption that g is distributed as a multivariate
gaussian, we can obtain the log likelihood the new patch
satisfies the model using
, matches the examples seen
in the training set. If we make the
(perhaps rash) assumption that g is distributed as a multivariate
gaussian, we can obtain the log likelihood the new patch
satisfies the model using
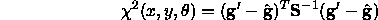
Locating a new component thus involves optimising 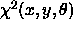 .
With any image noise this is a noisy function with many minima.
The global optima can be found approximately by testing at every position on
a suitably sized grid, at a range of angles. This can then be refined using
one of the local optimizers.
If we sample from the image using interpolation we can achieve sub-pixel
accuracy.
.
With any image noise this is a noisy function with many minima.
The global optima can be found approximately by testing at every position on
a suitably sized grid, at a range of angles. This can then be refined using
one of the local optimizers.
If we sample from the image using interpolation we can achieve sub-pixel
accuracy.
The initial approximation can be found more rapidly by a multi-resolution approach in which both model and image are smoothed with a range of filters [20].



