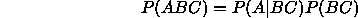
Starting with Bayes theorem we can extend the joint probability equation to three and more events
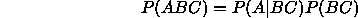
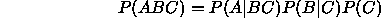
For n events with probabilities computed assuming a particular interpretation of the data Y (for example a model)
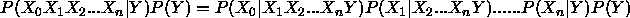
Maximum Likelihood statistics involves the identification of the
event Y which maximizes such a probability. In the absence of any
other information the prior probability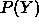 
is assumed to be
constant for all Y .
For large numbers of variables this is an impractical method for
probability estimation. Even if the events were simple binary
variables there are clearly an exponential number of possible values
for even the first term in 
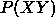requiring a prohibitive amount
of data storage.
In the case where each observed event is independent of all others
we can write.
Clearly this is a more practical definition of joint probability but the requirement of independence is quite a severe restriction. However, in some cases data can be analysed to remove these correlations, in particular the use of an appropriate data model (such as in least squares fitting) and processes for data orthogonalisation (including principle component analysis). For these reasons all common forms of maximum likelihood definitions assume data independence.
Probability independence is such an important concept it is worth
defining carefully. If knowledge of the probability of one variable
A allows us to gain knowledge about another event B then
these variables are not independent. Put in a way which is easily
visualised, if the distribution of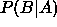 
over all possible
values of B is constant for all A then the two variables
are independent. Assumptions of independence of data can be tested
graphically by plotting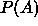 
against 
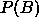or A against B
if the variables are directly monotonically related to their probabilities.
Unfortunately, under some circumstances, observable evidence towards a hypothesis cannot be combined into a single measure. Such problems are called Multi Objective problems, under such circumstances it may be impossible to define a unique solution to a problem and a whole set of candidate solution exist for various combinations of trade-off between the two objectives. This is best seen in the area of Genetic Algorithms where the set of optimal solutions lies along what is known as the Pareto Front. Further discussion of these techniques is beyond the scope of this tutorial, except to say that multi-objective optimization should be avoided if a probabilistic combination approach is applicable.