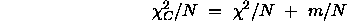
In some areas of machine vision the correct model required to describe a system can be derived without any real ambiguity. These situations are exemplified by the process of camera calibration where a good understanding of the physical processes involved allow us to define models which encompass the main optical and electronic effects. In other cases, however, selecting the correct model to describe a set of data is something that cannot be specified uniquely a-priori. Complicated models result in reduced ability to make predictions but simple models may not adequately describe the data. This is the problem of model selection and unfortunately it is endemic in much machine vision research eg: object recognition, tracking, segmentation, 3D modelling and in fact most scene interpretation schemes! Needless to say, if the wrong function is selected to describe a particular data set then the associated machine vision algorithm will fail and generally provide data which is of little or no use for subsequent processes. Generally fitting an arbitrary function to a set of unconstrained data without any attempt to verify the adequacy of the selected model should be treated with suspicion.
The problem of automatic model selection should be regarded as an important research topic and for the purposes of this tutorial I will only point out some standard approaches, their limitations and recent suggestions.
The standard method of least-squares fitting will give us an estimate of the optimal set of parameters to describe a given data set with a particular model, but unfortunately the Chi-squared measure is not directly suitable for model selection. The standard method for optimal model selection is that suggested by Akaike. He showed that the Chi-squared test statistic is biased towards small values due to the freedom that a model has to match the variation in the noise. An analysis for large data samples [14] shows that the bias could be estimated and compensated for using the test statistic:
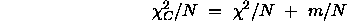
Where N is the quantity of data and m is the number of degrees of freedom for the parametric model. Under some limited circumstances this measure is sufficient to enable model selection but the method does have its limitations which are directly related to the definitions of the N and m terms and can best be understood by taking some extreme cases.
For example, take any model
with m parameters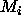 
where m is the number that we
believe we should be using in the Aikakie measure. Now
redefine the model to create a new parameter by splitting one of the
parameters to form two new ones 
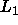and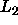 
such that
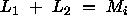. The new number of model parameters
is now m+1, thus the Akaike measure has changed without any change
in the descriptive power of the functional model.
At first sight such a manipulation may seem like a strange thing to do
but there are other (less obviously silly) ways of introducing correlations
between parameters in the definition of a model which are more
difficult to spot and much harder to eliminate. A 3x3 rotation matrix
for example has 9 free
parameters but only 3 degrees of freedom.
The problems are not limited to the model. Consider two data fits, both from N data but one with the data well distributed throughout the measurement domain and the other set tightly clustered. A well distributed data set can strongly constrain a set of model parameters but a tightly grouped set of data may not. Again the bias correction term is data dependent in a way that is not taken into account.
Both of the above problems have arisen because the bias correction term is only the limit of the bias and does not take account of data dependent variations, particularly for small data sets. Having said this, the Akaike measure can be successfully used for automatic model selection when "calibrated" on simulated data typical of the problem at hand by adjusting the process of estimation of N and m to give reasonable results. Over the years this approach has led to the generation of several "model selection" criteria for various applications.
These problems will also occur in any technique where it is assumed that the effects of function complexity are something that can be computed a-priori and are data independent. This includes recent techniques based on Shannon's information measures which attempt to include the effects of model complexity as prior terms in a Bayesian formalism described as the Minimum Description Length [2], which has been suggested for scene interpretation and segmentation. Again the performance of these approaches can be tuned to particular problems if the data set on which it is to work is understood sufficiently well in order to define the prior probabilities of function selection.
An alternative approach, which attempts to build in directly sensitivity
to data and parameter correlation, is based on a reinterpretation of
an existing measure the Bhattacharrya overlap.
.
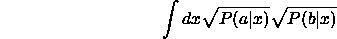
By re-interpretting the problem of model selection as one of optimal
prediction we can see immediately that the optimal model will be the one which
best predicts the current data set. By cauching this in probabilistic terms
we can then use the Bhattacharrya measure in order to perform model
selection. The Bhattacharrya (or Matusita) measure when applied to
the overlap of data and model prediction probability distributions
can be considered as a
chi-squared test statistic for a model with an infinite number
of degrees of freedom. Thus in relation to the work of Aikake the
measure requires no bias correction (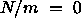 
). This measure has
already been successfully used to help solve the problems of object
recognition and feature tracking in machine vision [5,11]
and automatic self generation in neural networks [8].
Recent further extensions of this work will also be presented at this
conference.
Interestingly, the requirement that the function `concisely' fits the data (Figure 1) emerges as a data driven Maximim Likelihood mechanism and does not require any assumption regarding prior probabilities of function suitability.
Figure 1: Diagrams Illustrating Effects of Data Accuracy on Function Complexity