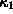Gaussian (K) and Mean (H) curvatures are the most widely used
indicators for surface shape classification in range image analysis. The HK
segmentation[1,2,4] was introduced by Besl
in 1986. He defines Gaussian and Mean curvatures, which are calculated
from the two principal curvatures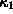 
and 
.
The Gaussian curvature equals the product of the principal curvatures.
The Mean curvature equals the arithmetic average of the principal
curvatures.
Image points can be labelled as belonging to a viewpoint- independent surface shape class type based on the combination of the signs from the Gaussian and Mean curvatures as shown in Table 1.
Table 1: Classification for the HK segmentation based on the
sign H and K
Koenderink defined an alternative curvature representation[3]. His
approach (SC classification) decouples the shape and the magnitude
of the curvedness. The surface in terms of relative curvature remains
invariant under changes in scale. He defined a shape index S, which
is a number in the range [-1,1]. The index covers all shapes except
for the planar shape which has an indeterminate shape index
(
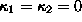). The shape index provides a continuous
gradation between shapes, such as concave shapes (-1 < S < -1/2),
hyperboloid shapes (-1/2 < S < 1/2) and convex shapes (1/2 < S < 1).
The image points can be classified as shown
in Table 2. We use the positive principal curvatures
(
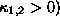for convex objects.
Beside the shape index, Koenderink introduced the positive value C for
describing the magnitude of the curvedness at a point. It is a
measure of how highly or gently curved a point is. At a point
that has no curvedness the value becomes zero.
Therefore, this variable can be used to recognise a plane surface.
Table 2: Classification for Koenderink's approach based on the
shape index (S)