Introduction

The problem of object recognition is often formulated as that of matching configurations of image features to configurations of model features. Such configurations are often represented as vertex-labeled graphs, whose nodes represent image features (or their abstractions), and whose edges represent relations (or constraints) between the features. For scale-space structures, represented as directed graphs, relations can represent both parent/child relations as well as sibling relations. To match two graph representations (hierarchical or otherwise) means to establish correspondences between their nodes. To evaluate the quality of a match, an overall distance measure is defined, whose value depends on both node and edge similarity. Previous work on graph matching has typically focused on the problem of finding a one-to-one correspondence between the vertices of two graphs. However, the assumption of one-to-one correspondence is a very restrictive one, for it assumes that the primitive features (nodes) in the two graphs agree in their level of abstraction. Unfortunately, there are a variety of conditions that may lead to graphs that represent visually similar image feature configurations yet do not contain a single one-to-one node correspondence. 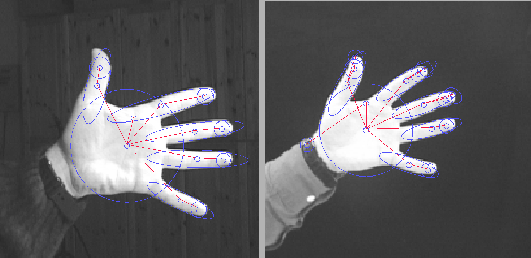The limitations of the one-to-one assumption are illustrated in Figure 1, in which an object is decomposed into a set of ridges and blobs extracted at appropriate scales [19]. The ridges and blobs map to nodes in a directed graph, with parent/child edges directed from coarser scale nodes to overlapping finer scale nodes, and sibling edges between nodes that share a parent. Although the two images clearly contain the same object, the decompositions are not identical. Specifically, the ends of the fingers in the right hand have been over-segmented with respect to the left hand. It is quite common that due to noise or segmentation errors, a single feature (node) in one graph can correspond to a collection of broken features (nodes) in another graph. Or, due to scale differences, a single, coarse-grained feature in one graph can correspond to a collection of fine-grained features in another graph. Hence, we seek not a one-to-one correspondence between image features (nodes), but rather a many-to-many correspondence.

Figure 1: The Need for Many-to-Many Matching. In the two images, the two objects are similar, but the extracted features are not necessarily one-to-one. Specifically, the ends of the fingers in the left hand have been over-segmented in the right hand.

In [10,7], we presented a framework for many-to-many matching of undirected graphs and directed graphs, respectively, where features and their relations were represented using edge-weighted graphs. The method began with transforming a graph into a metric tree. Next, using the graph embedding technique of Matousek [13], the tree was embedded into a normed vector space. This two-step transformation allowed us to reduce the problem of many-to-many graph matching to a much simpler problem of matching weighted distributions of points in a normed vector space. To compute the distance between two weighted distributions, we used a distribution-based similarity measure, known as the Earth Mover's Distance under transformation. The previous procedure suffered from a significant limitation. Namely, each graph was embedded into a vector space of arbitrary dimensions, and before the embeddings could be matched, a dimensionality reduction step was required, which was both costly and prone to error. Specifically, we used an inefficient Principal Components Analysis (PCA)-based method to project the two distributions into the same normed space. In this paper, we present an entirely different embedding method based on a spherical coding algorithm. This efficient (linear-time) method embeds metric trees into vector spaces of prescribed dimensionality, precluding the need for a dimensionality reduction step. We demonstrate the framework on the problem of multi-scale shape matching, in which an image is decomposed into a set of blobs and ridges with automatic scale selection.