Next: Construction of a Tree
Up: Metric Embedding of Graphs
Previous: Metric Embedding of Graphs
Our interest in low-distortion embedding is motivated by its ability
to transform the problem of many-to-many matching in finite graphs to
the problem of geometric point matching in low-dimensional vector
spaces. For graphs, the problem of low-distortion embedding is a
challenging one. Let
 ,
,
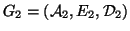 denote two graphs on vertex sets
denote two graphs on vertex sets  and
and 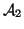 , edge sets
, edge sets 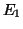 and
and 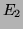 , under distance metrics
, under distance metrics 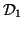 and
and 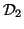 , respectively
(
, respectively
(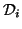 represents the distances between all pairs of nodes in
represents the distances between all pairs of nodes in 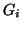 ).
Ideally, we seek a single embedding mechanism that can map each graph
to the same vector space, in which the two embeddings can be directly
compared.
We will tackle the problem in two steps. Given a
).
Ideally, we seek a single embedding mechanism that can map each graph
to the same vector space, in which the two embeddings can be directly
compared.
We will tackle the problem in two steps. Given a 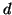 -dimensional target
space
-dimensional target
space
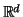 , we will seek low-distortion embeddings
, we will seek low-distortion embeddings 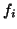 that map
sets
that map
sets 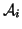 to sets
to sets 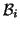 under distance function
under distance function  ,
,
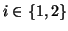 . The fixed-dimension embedding is based on a novel spherical
coding of the shortest-path metric on a tree. To apply this embedding
to our directed acyclic graphs therefore requires that we map them to
trees with low distortion. It is here that we introduce the concept
of relative scale to the points, allowing us to match hierarchical
graphs. Using these mappings, the problem of many-to-many
hierarchical vertex matching between
. The fixed-dimension embedding is based on a novel spherical
coding of the shortest-path metric on a tree. To apply this embedding
to our directed acyclic graphs therefore requires that we map them to
trees with low distortion. It is here that we introduce the concept
of relative scale to the points, allowing us to match hierarchical
graphs. Using these mappings, the problem of many-to-many
hierarchical vertex matching between  and
and 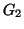 is
reduced to that of computing a mapping
is
reduced to that of computing a mapping 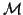 between subsets of
between subsets of  and
and 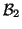 .
It is known that a minimum-distortion embedding of a metric tree into
the
.
It is known that a minimum-distortion embedding of a metric tree into
the 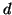 -dimensional Euclidean space will have distortion of
-dimensional Euclidean space will have distortion of
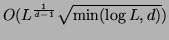 , where
, where 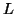 is the
number of leaves in the tree [8]. Observe that as
the dimension
is the
number of leaves in the tree [8]. Observe that as
the dimension 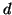 of the target space decreases, the distortion of the
embedding increases. We would therefore like to strike a good balance
between distortion and dimension.
of the target space decreases, the distortion of the
embedding increases. We would therefore like to strike a good balance
between distortion and dimension.
Next: Construction of a Tree
Up: Metric Embedding of Graphs
Previous: Metric Embedding of Graphs