Next: Construction of Spherical Codes
Up: Metric Embedding of Graphs
Previous: Problem Formulation
Construction of a Tree Metric for a Distance Function
Let
 denote an edge-weighted graph and
denote an edge-weighted graph and 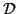 denote a
shortest-path metric for
denote a
shortest-path metric for  , i.e.,
, i.e.,
 , for all
, for all
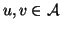 . The problem of approximating (or
fitting) an
. The problem of approximating (or
fitting) an 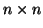 distance matrix
distance matrix 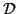 by a tree metric
by a tree metric
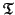 is
known as the Numerical Taxonomy problem. Since the numerical
taxonomy problem is an open problem for general distance metrics, we
must explore approximation methods.
The numerical taxonomy problem can be approximated by converting the
distance matrix
is
known as the Numerical Taxonomy problem. Since the numerical
taxonomy problem is an open problem for general distance metrics, we
must explore approximation methods.
The numerical taxonomy problem can be approximated by converting the
distance matrix 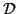 to the weaker ultra-metric distance matrix. To
create a general tree metric from an ultra-metric, we need to satisfy
the 4-point condition. Observe that a metric
to the weaker ultra-metric distance matrix. To
create a general tree metric from an ultra-metric, we need to satisfy
the 4-point condition. Observe that a metric 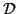 is additive
if and only if it is a tree metric (see [4]). Therefore, our
construction of a tree metric will consist of: 1) constructing an
ultra-metric from
is additive
if and only if it is a tree metric (see [4]). Therefore, our
construction of a tree metric will consist of: 1) constructing an
ultra-metric from 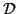 , and 2) modifying the ultra-metric to satisfy
the 4-point condition. For details of one such approximation
framework, see Agarwala et al. [1]. The construction of a
tree metric in their algorithm is achieved by transforming the general
tree metric problem to that of ultra-metrics. Their algorithm, which
follows the two-step procedure outlined above, generates an
approximation (tree metric
, and 2) modifying the ultra-metric to satisfy
the 4-point condition. For details of one such approximation
framework, see Agarwala et al. [1]. The construction of a
tree metric in their algorithm is achieved by transforming the general
tree metric problem to that of ultra-metrics. Their algorithm, which
follows the two-step procedure outlined above, generates an
approximation (tree metric
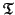 ) to an optimal additive metric in
time
) to an optimal additive metric in
time 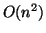 . It should be noted that this construction does not
necessarily maintain the vertex set of
. It should be noted that this construction does not
necessarily maintain the vertex set of  invariant. We will have to
make sure that in the embedding process (see
Section 4), the extra vertices
generated during the metric tree construction are eliminated. An
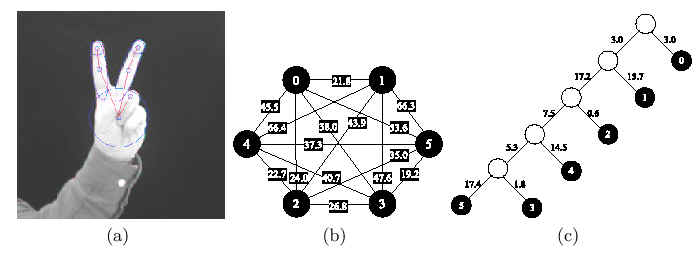
example of constructing a metric tree from a graph is shown
Figure 3.
invariant. We will have to
make sure that in the embedding process (see
Section 4), the extra vertices
generated during the metric tree construction are eliminated. An
example of constructing a metric tree from a graph is shown
Figure 3.
Figure 3:
Metric
tree representation of the Euclidean distances between nodes in a
graph. The gesture image (a) consists of 6 regions (the region
representing the entire hand is not shown). The complete graph in
(b) captures the Euclidean distances between the centroids of the
regions, while (c) is the metric tree representation of the
multi-scale decomposition (with additional vertices).
 |
Next: Construction of Spherical Codes
Up: Metric Embedding of Graphs
Previous: Problem Formulation

