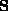For any motion, the relation eq:ambiguity implies that the form of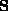 
is :
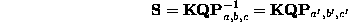
where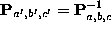 
commutes with 
.
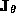When the rotation component of the displacement is performed around an axis parallel to the basis axes of the camera,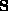 
takes special forms :
If the rotation axis is parallel to the horizontal axis of the camera : eq:Sx Q=(
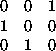
) and S S_x (
)
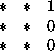
If the rotation axis is parallel to the vertical axis of the camera :
In practice, r is often negligible in comparison with k and we can consider that : eq:Sy S S_y (
)
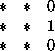
Finally, if the rotation axis is orthogonal to the image plane,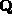 
is the identity and :
eq:Sz
S S_z (
)
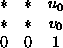
We can observe that, in these 3 cases, the structure of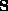 
is independent of any ambiguity in the real Jordan decomposition. It will be shown later that these cases correspond to critical motions for affine-to-Euclidean calibration.