 and
and 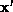 are corresponding image
points, then
are corresponding image
points, then



If  and
and 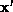 are corresponding image
points, then
are corresponding image
points, then
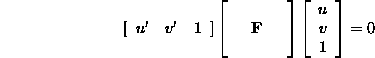
i.e. 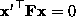 , where
, where 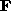 is the
is the
 fundamental matrix of maximum rank 2.
fundamental matrix of maximum rank 2.
Properties
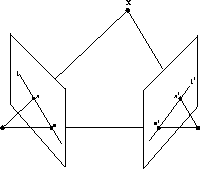

 is the
epipolar line corresponding
to
is the
epipolar line corresponding
to  , since
, since 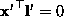 .
.

 is the
epipolar line corresponding
to
is the
epipolar line corresponding
to 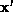 , since
, since  .
.




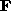 has 7 dof --- there are 9 matrix elements but only
their ratio is significant, which leaves 8 dof. In addition
the elements satisfy the constraint
has 7 dof --- there are 9 matrix elements but only
their ratio is significant, which leaves 8 dof. In addition
the elements satisfy the constraint 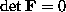 which leaves 7 dof.
which leaves 7 dof.
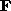 depends only on the direction of
translation
(unaffected by the magnitude of translation).
depends only on the direction of
translation
(unaffected by the magnitude of translation).
Example 1: Pure translation of a `fixed' camera
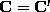 ,
, 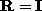 , then
, then
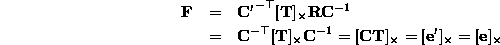

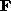 has only 2 dof corresponding to the position of the epipole.
has only 2 dof corresponding to the position of the epipole.
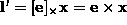 , and
, and 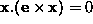 .
This is termed `auto-epipolar'.
.
This is termed `auto-epipolar'.




Connection with vanishing points The epipole is the vanishing point of the translation direction.

Example - pure translation continued If the camera translation is parallel to the x axis, then

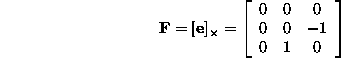
From 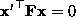
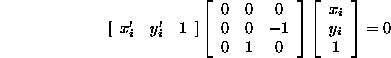
So that 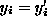 , i.e. the epipolar lines are corresponding rasters.
, i.e. the epipolar lines are corresponding rasters.