Computing F: II Least Squares Solutions

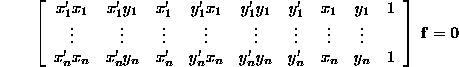
Given n corresponding points (n is typically hundreds) --- inevitably the points will be `` noisy'' and there will be mis-matches (outliers).

Linear solution --- ``The 8-point Algorithm''

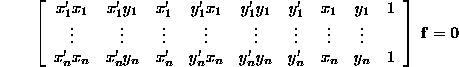
This equation will not be satisfied exactly (for n > 8). A solution is obtained by:

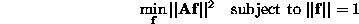
This is a standard linear algebra problem, the solution is the eigenvector with minimum eigenvalue of .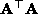

This computation is generally poorly conditioned, and it is very important to pre-condition the matrix: i.e. (affine) transform the image points:

where and are 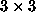matrices, such that

and < > indicates averages. A fundamental matrix 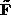is then computed from the transformed points 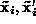and 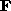obtained by

Pre-conditioning can make a difference of an order of magnitude to the average distance of a point from its epipolar lines (e.g. reduce an average of 3.5 to 0.3 pixels) and hundreds of pixels in the position of the epipoles.

Non-linear solution

Minimise (average) squared perpendicular distance of points from their epipolar lines:

where

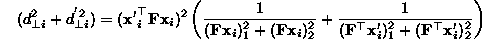
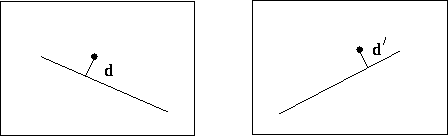
Use Levenberg-Marquardt or Powell for non-linear optimisation.

Summary Point

• Epipolar geometry is the fundamental geometric relationship between two images.
• It is represented algebraically by the fundamental matrix .
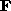• can be computed using image correspondences alone (7 or more).