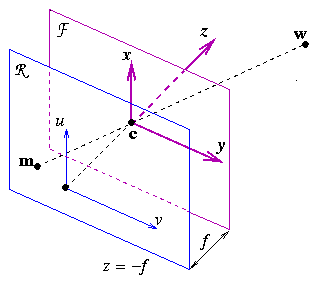
The camera is modelled by its optical centre 
and its
retinal plane (or image plane) 
. In each camera,
a 3-D point 
in world coordinates (where the
world coordinate frame is fixed arbitrarily) is projected into an
image point 
in camera coordinates, where 
is the intersection of with the line containing 
and . In projective (or homogeneous) coordinates, the
transformation from to is modelled by the linear
transformation 
where
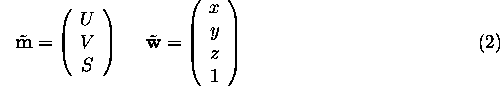
The points for which S=0 define the focal plane and
are projected to infinity.
|
Each pinhole camera is therefore modelled by its perspective
projection matrix (PPM) , which can be decomposed into
the product
The matrix 
gathers the intrinsic parameters of the
camera, and has the following form:
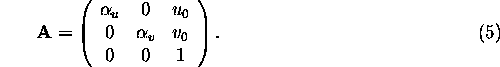
where 
are the focal lengths in vertical and
horizontal pixels, respectively, and 
are the coordinates
of the principal point. The matrix 
is composed by a
rotation matrix 
and a vector 
, encoding
the camera position and orientation (extrinsic parameters) in
the world reference frame, respectively:
Let us write the PPM as
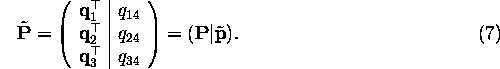
The plane 
(S=0) is
the focal plane, and the two planes 
and 
intersect
the retinal plane in the vertical (U=0) and horizontal (V=0) axis
of the retinal coordinates, respectively.
The optical centre is the intersection of the three
planes introduced in the previous paragraph; therefore
and
The optical ray associated to an image point is the line
, i.e. the set of points 
. The equation of this ray can
be written in parametric form as
with 
an arbitrary real number.
