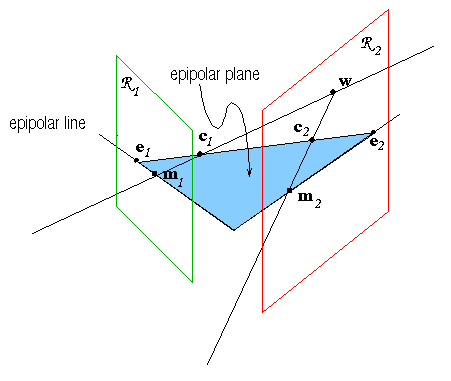
Let us consider a stereo rig composed by two pinhole cameras
(Fig. 2). Let 
and 
be the optical
centres of the two cameras. A 3D point 
is projected onto
both image planes, to points 
and 
, which
constitute a conjugate pair. Given a point in the left
image plane, its conjugate point in the right image is constrained to
lie on a line called the epipolar line (of ). This line is
the projection through of the optical ray of ;
indeed may be the projection of an arbitrary point on its
optical ray.
|
Furthermore one should observe that all the epipolar lines in one image plane pass through a common point called the epipole, which is the projection of the conjugate optical centre:
The parametric equation of the epipolar line of
writes:
In image coordinates it becomes:
where 
and
is the projection operator extracting the ith component from a
vector.
 |
 |
 |
 |
When is in the focal plane of the right camera, the right
epipole is at infinity, and the epipolar lines form a bundle of
parallel lines in the right image. Analytically, the direction of each
epipolar line can be obtained by taking the derivative of the
parametric equations (13,14) with respect to
:
Note that the denominator is the same in both components, hence it
does not affect the direction of the vector. The epipole is rejected
to infinity when 
. In this case, the direction
of the epipolar lines in the right image doesn't depend on 
any more and all the epipolar lines becomes parallel to vector
.
A very special case is when both epipoles are at infinity, that
happens when the line containing and (the
baseline) is contained in both focal planes, or the retinal planes
are parallel to the baseline. Epipolar lines form a bundle of parallel
lines in both images.
Any pair of images can be transformed so that epipolar lines are parallel and horizontal in each image as in Fig. 3. This procedure is called rectification.
