

Next: The rectifying transformation
Up: Epipolar Rectification
Previous: Camera model and epipolar
Rectification of camera matrices
We assume that the stereo rig is calibrated, i.e., the PPMs
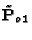 and
and
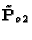 are known. The idea
behind rectification is to define two new PPMs
are known. The idea
behind rectification is to define two new PPMs
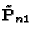 and
and
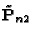 obtained by rotating the old ones around
their optical centers until focal planes becomes coplanar, thereby
containing the baseline. This ensures that epipoles are at infinity,
hence epipolar lines are parallel. To have horizontal
epipolar lines, the baseline must be parallel to the new X axis
of both cameras. In addition, to have a proper rectification,
conjugate points must have the same vertical coordinate. This
is obtained by requiring that the new cameras have the same intrinsic
parameters. Note that, being the focal length the same, retinal planes
are coplanar too, as in Figure 2.
obtained by rotating the old ones around
their optical centers until focal planes becomes coplanar, thereby
containing the baseline. This ensures that epipoles are at infinity,
hence epipolar lines are parallel. To have horizontal
epipolar lines, the baseline must be parallel to the new X axis
of both cameras. In addition, to have a proper rectification,
conjugate points must have the same vertical coordinate. This
is obtained by requiring that the new cameras have the same intrinsic
parameters. Note that, being the focal length the same, retinal planes
are coplanar too, as in Figure 2.
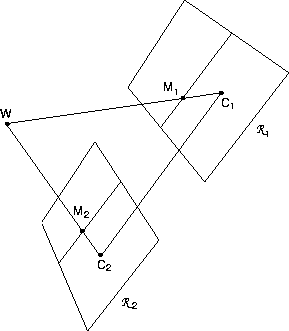
Figure 2:
Rectified cameras. Retinal planes are coplanar and parallel
to the baseline.
 |
In summary: positions (i.e, optical centers) of the new PPMs are the
same as the old cameras, whereas the new orientation (the same for
both cameras) differs from the old ones by suitable rotations;
intrinsic parameters are the same for both cameras. Therefore, the
two resulting PPMs will differ only in their optical centers, and they
can be thought as a single camera translated along the X axis of
its reference system.
Let us write the new PPMs in terms of their factorization. From
(2) and (7):
![\begin{displaymath}\tilde{\bf P}_{n1} = {\bf A} [{\bf R}\; \vert- {\bf R} \; {\b...
...bf P}_{n2} = {\bf A} [{\bf R}\; \vert- {\bf R} \; {\bf c}_2] .
\end{displaymath}](img39.gif) |
(9) |
The intrinsic parameters matrix 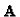 is the same for both PPMs,
and can be chosen arbitrarily (see MATLAB code). The optical
centers
is the same for both PPMs,
and can be chosen arbitrarily (see MATLAB code). The optical
centers  and
and  are given by the old optical
centers, computed with (6). The matrix
are given by the old optical
centers, computed with (6). The matrix 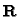 ,
which gives the camera's pose, is the same for both PPMs. It will be
specified by means of its row vectors
,
which gives the camera's pose, is the same for both PPMs. It will be
specified by means of its row vectors
 |
(10) |
that are the X, Y, and Z axes, respectively, of the
camera reference frame, expressed in world coordinates.
According to the previous comments, we take:
- 1.
- The new X axis parallel to the baseline:
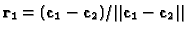
- 2.
- The new Y axis orthogonal to X (mandatory) and to
 :
:
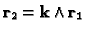
- 3.
- The new Z axis orthogonal to XY (mandatory) :
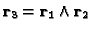
In point 2,  is an arbitrary unit vector, that fixes the
position of the new Y axis in the plane orthogonal to X. We take it equal to the Z unit vector of the old left
matrix, thereby constraining the new Y axis to be orthogonal to
both the new X and the old left Z.
is an arbitrary unit vector, that fixes the
position of the new Y axis in the plane orthogonal to X. We take it equal to the Z unit vector of the old left
matrix, thereby constraining the new Y axis to be orthogonal to
both the new X and the old left Z.
This algorithm fails when the optical axis is parallel to the
baseline, i.e., when there is a pure forward motion.


Next: The rectifying transformation
Up: Epipolar Rectification
Previous: Camera model and epipolar
Andrea Fusiello
2000-03-17

