

Next: Varying intrinsic parameters
Up: Uncalibrated Euclidean Reconstruction
Previous: Autocalibration
Subsections
Stratification
Let us assume that a projective reconstruction is available, that is a
sequence
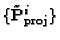 of camera matrices
such that:
of camera matrices
such that:
![\begin{displaymath}\tilde{\bf P}^0_{\mathrm{proj}} = [{\bf I} \;\vert\; {\bf0}] ...
...{\bf P}^i_{\mathrm{proj}} = [{\bf Q}^i \;\vert\; {\bf
q}^i] .
\end{displaymath}](img91.gif) |
(24) |
We are looking for a Euclidean reconstruction, that is a
 nonsingular matrix
nonsingular matrix
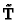 that upgrades the projective
reconstruction to Euclidean. If
that upgrades the projective
reconstruction to Euclidean. If
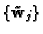 is the sought Euclidean
structure,
is the sought Euclidean
structure,
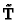 must be such that:
must be such that:
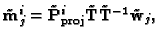 hence
hence
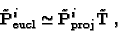 |
(25) |
where the symbol 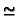 means ``equal up to a scale factor.''
means ``equal up to a scale factor.''
Projective reconstruction differs from Euclidean by an unknown
projective transformation in the 3-D projective space, which can be
seen as a suitable change of basis. Thanks to the fundamental theorem
of projective geometry [41], a collineation in space is
determined by five points, hence the knowledge of the true (Euclidean)
position of five points allows to compute the unknown 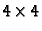 matrix
matrix
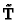 that transform the Euclidean frame into the
projective frame.
Moreover, if intrinsic parameters
that transform the Euclidean frame into the
projective frame.
Moreover, if intrinsic parameters 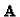 are known, then
are known, then
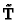 can be computed by solving a linear system of equations (see
(54) in Sec. 5.2.5).
can be computed by solving a linear system of equations (see
(54) in Sec. 5.2.5).
The challenging problem is to recover
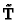 without
additional information, using only the hypothesis of constant
intrinsic parameters. The works by Hartley [17], Pollefeys
and Van Gool [37], Heyden and Åström [20], Triggs
[46] and Bougnoux [4] will be reviewed, but first we
will make some remarks that are common to most of the methods.
without
additional information, using only the hypothesis of constant
intrinsic parameters. The works by Hartley [17], Pollefeys
and Van Gool [37], Heyden and Åström [20], Triggs
[46] and Bougnoux [4] will be reviewed, but first we
will make some remarks that are common to most of the methods.
We can choose the first Euclidean-calibrated camera to be
![$ \tilde{\bf
P}^0_\mathrm{eucl} = {\bf A} [{\bf I} \;\vert\; {\bf0}] $](img95.gif) ,
thereby fixing
arbitrarily the rigid transformation:
,
thereby fixing
arbitrarily the rigid transformation:
![\begin{displaymath}\tilde{\bf P}^0_{\mathrm{eucl}} = {\bf A} [{\bf I} \;\vert\; ...
...^i_{\mathrm{eucl}} = {\bf A} [{\bf R}^i \;\vert\; {\bf t}^i] .
\end{displaymath}](img96.gif) |
(26) |
With this choice, it is easy to see that
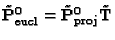 implies
implies
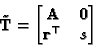 |
(27) |
where
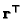 is an arbitrary vector of three elements
is an arbitrary vector of three elements
![$ [r_1 \;
r_2 \; r_3]$](img100.gif) .
Under this parameterization
.
Under this parameterization
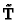 is clearly non
singular, and being defined up to a scale factor, it depends on eight
parameters (let s=1).
is clearly non
singular, and being defined up to a scale factor, it depends on eight
parameters (let s=1).
Substituting (24) in (25) one
obtains
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{eucl}} \simeq\tilde{\bf P}^i_{\mathr...
...bf Q}^i{\bf A} + {\bf q}^i {\bf r}^\top\;\vert\; {\bf
q}^i ] ,
\end{displaymath}](img101.gif) |
(28) |
and from (26)
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{eucl}} = {\bf A} [{\bf R}^i \;\vert\; {\bf t}^i] =
[ {\bf A} {\bf R}^i \;\vert\; {\bf A}{\bf t}^i] ,
\end{displaymath}](img102.gif) |
(29) |
hence
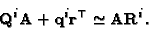 |
(30) |
This is the basic equation, relating the unknowns 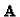 (five
parameters) and
(five
parameters) and 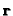 (three parameters) to the available data
(three parameters) to the available data 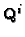 and
and 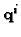 .
.
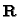 is unknown, but must be a rotation
matrix.
is unknown, but must be a rotation
matrix.
Equation (30) can be rewritten as
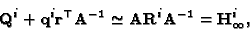 |
(31) |
relating the unknown vector
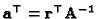 to
the homography of the infinity plane (compare (31) with
(18)). It can be seen that
to
the homography of the infinity plane (compare (31) with
(18)). It can be seen that
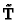 factorizes as
follows
factorizes as
follows
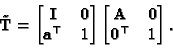 |
(32) |
The right-hand matrix is an affine transformation, not moving the
infinity plane, whereas the left-hand one is a transformation moving
the infinity plane.
Substituting the latter into (25) we obtain:
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{eucl}}
\begin{bmatrix}
{\bf A}^{-1}...
...&1\\
\end{bmatrix} = [{\bf H}_{\infty}^{i} \vert {\bf q}^{i}]
\end{displaymath}](img110.gif) |
(33) |
Therefore, the knowledge of the homography of the infinity plane
(given by 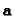 )
allows to compute the Euclidean structure up to
an affine transformation, that is an affine reconstruction.
)
allows to compute the Euclidean structure up to
an affine transformation, that is an affine reconstruction.
Another useful observation is, if
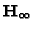 is known and the
intrinsic parameters are constant, the intrinsic parameters matrix
is known and the
intrinsic parameters are constant, the intrinsic parameters matrix
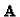 can easily be computed
[1,17,30,49].
can easily be computed
[1,17,30,49].
Let us consider the case of two cameras. If
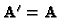 ,
then
,
then
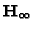 is exactly known (with the right scale), since
is exactly known (with the right scale), since
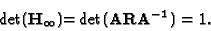 |
(34) |
From (17) we obtain
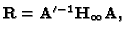 and, since
and, since
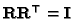 ,
it is easy to obtain:
,
it is easy to obtain:
 |
(35) |
where
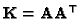 is the Kruppa coefficients
matrix. As (35) is an equality between
is the Kruppa coefficients
matrix. As (35) is an equality between
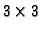 symmetric matrices, we obtain a linear system of six equations in the
five unknown k1, k2,
k3, k4, k5 . In fact, only four
equations are independent [30,49], hence at least
three views (with constant intrinsic parameters) are required to
obtain an over-constrained linear system, which can be easily solved
with a linear least-squares technique.
symmetric matrices, we obtain a linear system of six equations in the
five unknown k1, k2,
k3, k4, k5 . In fact, only four
equations are independent [30,49], hence at least
three views (with constant intrinsic parameters) are required to
obtain an over-constrained linear system, which can be easily solved
with a linear least-squares technique.
Note that two views would be sufficient under the usual assumption
that the image reference frame is orthogonal (
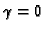 ), which
gives the additional constraint
k3 k5 = k2.
), which
gives the additional constraint
k3 k5 = k2.
If points at infinity (in practice, sufficiently far from the camera)
are in the scene,
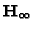 can be computed from point
correspondences, like any ordinary plane homography
[49]. Moreover, with additional knowledge, it can be
estimated from vanishing points or parallelism
[7,9], or constrained motion [1].
can be computed from point
correspondences, like any ordinary plane homography
[49]. Moreover, with additional knowledge, it can be
estimated from vanishing points or parallelism
[7,9], or constrained motion [1].
In the rest of the section, some of the most promising stratification
techniques will be reviewed.
Hartley [17] pioneered this kind of approach. Starting from
(30), we can write
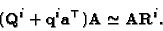 |
(36) |
By taking the QR decomposition of the left-hand side we obtain an
upper triangular matrix 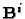 such that
such that
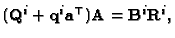 so (36)
rewrites
so (36)
rewrites
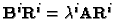 or
or
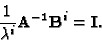 |
(37) |
The scale factor
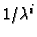 can be chosen so that the sum of the
squares of the diagonal entries of
can be chosen so that the sum of the
squares of the diagonal entries of
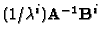 equals three.
We seek
equals three.
We seek 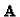 and
and 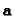 that minimizes
that minimizes
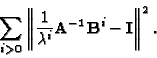 |
(38) |
Each camera excluding the first, gives six constraints in eight
unknowns, so three cameras are sufficient. In practice there are more
than three cameras, and the non-linear least squares problem can be
solved with Levenberg-Marquardt minimization algorithm [12]. As
noticed in the case of Kruppa equations, a good initial guess for the
unknowns 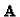 and
and 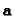 is needed in order for the algorithm
to converge to the solution.
is needed in order for the algorithm
to converge to the solution.
Given that from
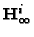 the computation of
the computation of 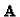 is
straightforward, a guess for
is
straightforward, a guess for 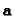 (that determines
(that determines
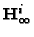 )
is sufficient. The cheirality constraints
[14] are exploited by Hartley to estimate the infinity plane
homography, thereby obtaining an approximate affine (or
quasi-affine) reconstruction.
)
is sufficient. The cheirality constraints
[14] are exploited by Hartley to estimate the infinity plane
homography, thereby obtaining an approximate affine (or
quasi-affine) reconstruction.
In this approach [37], a projective reconstruction is first
updated to affine reconstruction by the use of the modulus
constraint [30,38]: since the left-hand part of
(31) is conjugated to a (scaled) rotation matrix, all
eigenvalues must have equal moduli. Note that this holds if and only
if intrinsic parameters are constant. To make the constraint explicit
we write the characteristic polynomial:
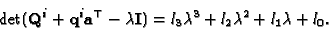 |
(39) |
The equality of the roots of the characteristic polynomial is not
easy to impose, but a simple necessary condition holds:
This yields a fourth order polynomial equation in the unknown 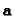 for each camera except the first, so a finite number of solutions
can be found for four cameras. Some solutions will be discarded using
the modulus constraint, that is more stringent than (40).
for each camera except the first, so a finite number of solutions
can be found for four cameras. Some solutions will be discarded using
the modulus constraint, that is more stringent than (40).
As discussed previously, autocalibration is achievable with only
three views. It is sufficient to note that, given three cameras, for
every plane homography, the following holds [30]:
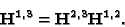 |
(41) |
In particular it holds for the infinity plane homography, so
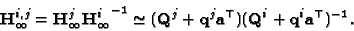 |
(42) |
In this way we obtain a constraint on the plane at infinity for each
pair of views. Let us write the characteristic polynomial:
Writing the constraint (40) for the three views, a system
of three polynomial of degree four in three unknowns is obtained.
Here, like in the solution of Kruppa equations, homotopy continuation
methods could be applied to compute all the 43 = 64 solutions.
In practice more than three views are available, and we must solve a
non-linear least-squares problem: Levenberg-Marquardt minimization is used by the
author.
The method proposed by Heyden and Åström [20] is again based on
(30), which can be rewritten as
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{proj}} \left [ \begin {array}{c}
{\...
...\bf r}^\top\\
\end {array}\right]
\simeq{\bf A} {\bf R}^i .
\end{displaymath}](img133.gif) |
(45) |
Since
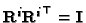 it follows that:
it follows that:
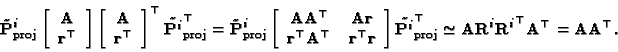 |
(46) |
The constraints expressed by (46) are called the Kruppa
constraints [20]. Note that (46) contains five
equations, because the matrices of both members are symmetric, and the
homogeneity reduces the number of equations with one. Hence, each
camera matrix, apart from the first one, gives five equations in the
eight unknowns
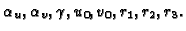 A unique solution is obtained when three cameras are available. If
the unknown scale factor is introduced explicitly, (46)
rewrites:
A unique solution is obtained when three cameras are available. If
the unknown scale factor is introduced explicitly, (46)
rewrites:
![\begin{displaymath}0 = f_i({\bf A},{\bf r},\lambda_i) = \lambda_i^2 {\bf A} {\bf...
...
\end {array}\right]
\tilde{{\bf P}^i}^\top_{\mathrm{proj}} .
\end{displaymath}](img137.gif) |
(47) |
Therefore, 3 cameras yield 10 equations in 8 unknowns.
Triggs [46] proposed a method based on the absolute
quadric and, independently from Heyden and Åström, he derived an equation
closely related to (46). The absolute quadric
 consists of planes tangent to the absolute conic
[6], and in a Euclidean frame, is represented by the matrix
consists of planes tangent to the absolute conic
[6], and in a Euclidean frame, is represented by the matrix
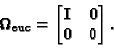 |
(48) |
If
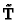 is a projective transformation acting as in
(25), then it can be verified [46] that it
transforms
is a projective transformation acting as in
(25), then it can be verified [46] that it
transforms
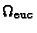 into
into
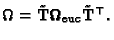 Since the projection of the
absolute quadric yields the dual image of the absolute conic
[46], one obtain
Since the projection of the
absolute quadric yields the dual image of the absolute conic
[46], one obtain
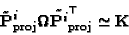 |
(49) |
from which, using (27), (46) follows
immediately. Triggs, however, does not assume any particular form for
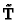 ,
hence the unknown are
,
hence the unknown are 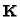 and
and
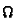 .
Note that both these matrix are symmetric and defined up to
a scale factor.
.
Note that both these matrix are symmetric and defined up to
a scale factor.
Let 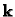 be the matrix composed by the the six elements of the
lower triangle of
be the matrix composed by the the six elements of the
lower triangle of 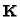 ,
and
,
and
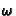 be the matrix
composed by the six elements of the lower triangle of
be the matrix
composed by the six elements of the lower triangle of
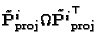 ,
then (49) is tantamount to
saying that the two vectors are equal up to a scale, hence
,
then (49) is tantamount to
saying that the two vectors are equal up to a scale, hence
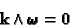 |
(50) |
in which the unknown scale factor is eliminated. For each camera this
amounts to 15 bilinear equations in 9+5 unknowns, since both 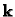 and
and
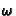 are defined up to a scale factor. Since only
five of them are linearly independent, at least three images are
required for a unique solution.
are defined up to a scale factor. Since only
five of them are linearly independent, at least three images are
required for a unique solution.
Triggs uses two methods for solving the non-linear least-squares
problem: sequential quadratic programming [12] on 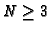 cameras, and a quasi-linear method with SVD factorization on
cameras, and a quasi-linear method with SVD factorization on 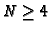 cameras. He recommend to use data standardization [15] and
to enforce
cameras. He recommend to use data standardization [15] and
to enforce
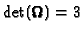 .
The sought transformation
.
The sought transformation
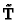 is computed by taking the eigen-decomposition of
is computed by taking the eigen-decomposition of
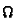 .
.
Bougnoux
This methods [4] is different from the previous ones,
because it does not require constant intrinsic parameters and because
it achieves only an approximate Euclidean reconstruction, without obtaining
meaningful camera parameters as a by-product.
Let us write (25) in the following form:
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{eucl}}
=\left[
\begin{array}{c\vert...
...ay}\right ]\simeq\tilde{\bf P}^i_{\mathrm{proj}}\tilde{\bf T}
\end{displaymath}](img150.gif) |
(51) |
where
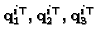 are
the rows of
are
the rows of
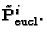 The usual assumptions
The usual assumptions
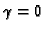 and
and
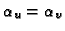 ,
are used to constraint the
Euclidean camera matrices:
,
are used to constraint the
Euclidean camera matrices:
Thus each camera, excluding the first, gives two constraints of degree
four. Since we have six unknown, at least four cameras are required to
compute
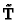 .
If the principal point
(u0, v0) is forced
to the image center, the unknowns reduce to four and only three cameras are
needed.
.
If the principal point
(u0, v0) is forced
to the image center, the unknowns reduce to four and only three cameras are
needed.
The non-linear minimization required to solve the resulting system is
rather unstable and must be started close to the solution: an estimate
of the focal length and 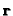 is needed. Assuming known principal
point, no skew, and unit aspect ratio, the focal length
is needed. Assuming known principal
point, no skew, and unit aspect ratio, the focal length 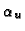 can
be computed from the Kruppa equations in closed form [4].
Then, given the intrinsic parameters
can
be computed from the Kruppa equations in closed form [4].
Then, given the intrinsic parameters 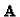 ,
an estimate of
,
an estimate of 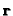 can be computed by solving a linear least-squares problem.
From (46) the following is obtained:
can be computed by solving a linear least-squares problem.
From (46) the following is obtained:
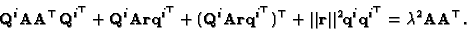 |
(54) |
Since
![$[{\bf A} {\bf A}^\top]_{3,3}={\bf K}_{3,3}=1,$](img160.gif) then
then 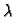 is
fixed. After some algebraic manipulation [4], one ends up
with four linear equations in
is
fixed. After some algebraic manipulation [4], one ends up
with four linear equations in 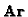 .
This method works also with
varying intrinsic parameters, although, in practice, only the focal
length is allowed to vary, since principal point is forced to the
image center and no skew and unit aspect ratio are assumed. The
estimation of the camera parameters is inaccurate, nevertheless
Bougnoux proves that the reconstruction is correct up to an
anisotropic homotethy, which he claims to be enough for the
reconstructed model to be usable.
.
This method works also with
varying intrinsic parameters, although, in practice, only the focal
length is allowed to vary, since principal point is forced to the
image center and no skew and unit aspect ratio are assumed. The
estimation of the camera parameters is inaccurate, nevertheless
Bougnoux proves that the reconstruction is correct up to an
anisotropic homotethy, which he claims to be enough for the
reconstructed model to be usable.
Methods based on stratification have appeared only recently, and only
preliminary and partial results are available. In many cases they
show a graceful degradation as noise increases, but the issue of
initialization is not always addressed.
Hartley's algorithm leads to a minimization problem that requires a
good initial guess; this is computed using a quite complicated method,
involving the cheirality constraints. Pollefeys-VanGool's algorithm
leads to an easier minimization, and this justify the claim that
convergence toward a global minimum is relatively easily obtained. It
is unclear, however, how the initial guess has to be chosen. The
method proposed by Heyden and Åström was evaluated only on one example, and was
initialized close to the ground-truth. Experiments on synthetic data
reported by Triggs, suggest that his non-linear algorithm is stable
and requires only approximate initialization (the author reports that
initial calibration may be wrong up to 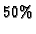 ).
Bougnoux's algorithm is quite different form the others, since its
goal is not to obtain an accurate Euclidean reconstruction. Assessment
of reconstruction quality is only visual.
).
Bougnoux's algorithm is quite different form the others, since its
goal is not to obtain an accurate Euclidean reconstruction. Assessment
of reconstruction quality is only visual.


Next: Varying intrinsic parameters
Up: Uncalibrated Euclidean Reconstruction
Previous: Autocalibration
Andrea Fusiello
2000-03-16
![]() of camera matrices
such that:
of camera matrices
such that:
![]() matrix
matrix
![]() that transform the Euclidean frame into the
projective frame.
Moreover, if intrinsic parameters
that transform the Euclidean frame into the
projective frame.
Moreover, if intrinsic parameters ![]() are known, then
are known, then
![]() can be computed by solving a linear system of equations (see
(54) in Sec. 5.2.5).
can be computed by solving a linear system of equations (see
(54) in Sec. 5.2.5).
![]() without
additional information, using only the hypothesis of constant
intrinsic parameters. The works by Hartley [17], Pollefeys
and Van Gool [37], Heyden and Åström [20], Triggs
[46] and Bougnoux [4] will be reviewed, but first we
will make some remarks that are common to most of the methods.
without
additional information, using only the hypothesis of constant
intrinsic parameters. The works by Hartley [17], Pollefeys
and Van Gool [37], Heyden and Åström [20], Triggs
[46] and Bougnoux [4] will be reviewed, but first we
will make some remarks that are common to most of the methods.
![]() ,
thereby fixing
arbitrarily the rigid transformation:
,
thereby fixing
arbitrarily the rigid transformation:
![]() ,
then
,
then
![]() is exactly known (with the right scale), since
is exactly known (with the right scale), since
![]() ), which
gives the additional constraint
k3 k5 = k2.
), which
gives the additional constraint
k3 k5 = k2.
![]() can be computed from point
correspondences, like any ordinary plane homography
[49]. Moreover, with additional knowledge, it can be
estimated from vanishing points or parallelism
[7,9], or constrained motion [1].
can be computed from point
correspondences, like any ordinary plane homography
[49]. Moreover, with additional knowledge, it can be
estimated from vanishing points or parallelism
[7,9], or constrained motion [1].
![]() can be chosen so that the sum of the
squares of the diagonal entries of
can be chosen so that the sum of the
squares of the diagonal entries of
![]() equals three.
We seek
equals three.
We seek ![]() and
and ![]() that minimizes
that minimizes
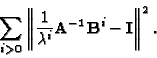
![]() the computation of
the computation of ![]() is
straightforward, a guess for
is
straightforward, a guess for ![]() (that determines
(that determines
![]() )
is sufficient. The cheirality constraints
[14] are exploited by Hartley to estimate the infinity plane
homography, thereby obtaining an approximate affine (or
quasi-affine) reconstruction.
)
is sufficient. The cheirality constraints
[14] are exploited by Hartley to estimate the infinity plane
homography, thereby obtaining an approximate affine (or
quasi-affine) reconstruction.
![]() consists of planes tangent to the absolute conic
[6], and in a Euclidean frame, is represented by the matrix
consists of planes tangent to the absolute conic
[6], and in a Euclidean frame, is represented by the matrix
![]() be the matrix composed by the the six elements of the
lower triangle of
be the matrix composed by the the six elements of the
lower triangle of ![]() ,
and
,
and
![]() be the matrix
composed by the six elements of the lower triangle of
be the matrix
composed by the six elements of the lower triangle of
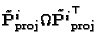 ,
then (49) is tantamount to
saying that the two vectors are equal up to a scale, hence
,
then (49) is tantamount to
saying that the two vectors are equal up to a scale, hence
![]() cameras, and a quasi-linear method with SVD factorization on
cameras, and a quasi-linear method with SVD factorization on ![]() cameras. He recommend to use data standardization [15] and
to enforce
cameras. He recommend to use data standardization [15] and
to enforce
![]() .
The sought transformation
.
The sought transformation
![]() is computed by taking the eigen-decomposition of
is computed by taking the eigen-decomposition of
![]() .
.
![\begin{displaymath}\tilde{\bf P}^i_{\mathrm{eucl}}
=\left[
\begin{array}{c\vert...
...ay}\right ]\simeq\tilde{\bf P}^i_{\mathrm{proj}}\tilde{\bf T}
\end{displaymath}](img150.gif)
![]() is needed. Assuming known principal
point, no skew, and unit aspect ratio, the focal length
is needed. Assuming known principal
point, no skew, and unit aspect ratio, the focal length ![]() can
be computed from the Kruppa equations in closed form [4].
Then, given the intrinsic parameters
can
be computed from the Kruppa equations in closed form [4].
Then, given the intrinsic parameters ![]() ,
an estimate of
,
an estimate of ![]() can be computed by solving a linear least-squares problem.
From (46) the following is obtained:
can be computed by solving a linear least-squares problem.
From (46) the following is obtained: