This tutorial is generated as a set of HTML pages. If you want to
print the tutorial, please use the
PDF
version.
The theory for operators describing rotational symmetries in image regions using orientation information was developed around 1981 by Granlund and Knutsson. It was however first mentioned in a patent from 1986, see [18,17,19]. An early related work is also [14]. For a more thorough description, see e.g. [15,6,4,12]. See also [5,3,22,2,1,21].
The theory describes modelling and detection of complex curvature, e.g. corners, circular, and star-shaped patterns. The description is based on a local orientation description in double angle representation.
The symmetries can be described in a manner invariant to color, and
whether the patterns consist of edges or lines.
These symmetries can serve as points-of-interest features for various
computer vision tasks. Applications involve object recognition
[15], recognition of object view [10], finding
the non-visible center of the annual rings of a tree
[20], generation of potential fields indicating
possible locations for objects [21], and detection of
landmarks in aerial images for use in navigation [13].
The rotational symmetries are related to the Generalized Hough
Transform, GHT, which uses edges and their orientation to detect
curvature, e.g. circles (see [8]). The difference is that in
the GHT only positive votes give a contribution, while in the complex
valued correlation used to detect rotational symmetries we will also
get negative votes (see [6]). The rotational symmetries can
also be more efficiently computed than the GHT.
The double angle representation of local orientation, ![]() , is defined
as a vector, or complex number, with a phase that is double the local
orientation, see [11]. Figure 1 illustrates
the idea.
, is defined
as a vector, or complex number, with a phase that is double the local
orientation, see [11]. Figure 1 illustrates
the idea.
The computer vision literature describes a number of methods to detect edges, lines, and local orientation. A convenient way to compute edges in the double angle representation is to use the image gradient:
By using the double angle representation we avoid ambiguities in the
representation of boundaries between vector fields, e.g. regions in
color images. It does not matter if we choose to say that the
orientation has the direction ![]() or, equivalently,
or, equivalently,
![]() . In the double angle representation both choices get the same
descriptor
. In the double angle representation both choices get the same
descriptor
![]() . Also, averaging the double angle
description field makes sense. One can argue that two orthogonal
orientations should have maximally different representations,
e.g. vectors that point in opposite directions.
. Also, averaging the double angle
description field makes sense. One can argue that two orthogonal
orientations should have maximally different representations,
e.g. vectors that point in opposite directions.
There are many classes of patterns and symmetries that can be
described using the local orientation in double angle representation.
One class of symmetries, called the rotational symmetries, is
defined as follows:
Definition: Let ![]() denote polar coordinates. A signal
denote polar coordinates. A signal
![]() is called a rotational symmetry if
is called a rotational symmetry if
![]() only depends on
only depends on ![]() , where
, where ![]() is the local orientation
description in double angle representation of the signal
is the local orientation
description in double angle representation of the signal ![]() .
.
Special cases are the ![]() :th order symmetries:
:th order symmetries:
Many other useful patterns can be described as linear combinations of
the ![]() :th order symmetries (c.f. polar Fourier transform):
:th order symmetries (c.f. polar Fourier transform):
![\includegraphics[width=11cm]{rotsym_spectrum}](img50.gif)
|
The rotational symmetries are detected in a hierarchical manner. Figure 5 illustrates the idea on a simple binary test image. Note the color representation of the complex valued images. Also note that the double angle representation is non-linear, which means that the algorithm is not equivalent to linear filtering directly on the image.
|
First, the local orientation is computed and represented by the double
angle, e.g. by using equation 1. Second, the symmetries
are detected from the local orientation. One way to detect the ![]() :th
order symmetry is to simply correlate the orientation image
:th
order symmetry is to simply correlate the orientation image ![]() with
the filter
with
the filter
![]() , i.e.
, i.e.
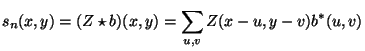 |
(4) |
Another, more efficient, way to compute the symmetries is
to use the parameters from a local polynomial expansion model of ![]() .
A second degree polynomial is sufficient to detect symmetries of order
.
A second degree polynomial is sufficient to detect symmetries of order
![]() :
:
| (5) |
From the parameters
![]() we compute the
symmetry responses
we compute the
symmetry responses ![]() ,
, ![]() ,
, ![]() as
as
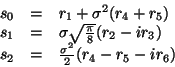 |
(6) |
Sometimes it may be desirable to classify the response into one
symmetry order ![]() , for example if we want to use
, for example if we want to use ![]() as a detector
for curvature and corners, and
as a detector
for curvature and corners, and ![]() as a detector for circle and
star shapes. As can be seen in figure 3, the first order
symmetries also approximately include linear symmetries. The same
overlap holds between other symmetries (corners give for example a
fairly high magnitude
as a detector for circle and
star shapes. As can be seen in figure 3, the first order
symmetries also approximately include linear symmetries. The same
overlap holds between other symmetries (corners give for example a
fairly high magnitude ![]() , because they are approximately ``half
circles'' etc.).
Hence, to further make the responses more selective we can apply an
inhibition scheme. The basic idea is that if one magnitude is high,
the other ones should get low. See [15] and [16] for
suggestions on how to implement this.
, because they are approximately ``half
circles'' etc.).
Hence, to further make the responses more selective we can apply an
inhibition scheme. The basic idea is that if one magnitude is high,
the other ones should get low. See [15] and [16] for
suggestions on how to implement this.