


Next: Background
Up: Image Processing: Flows under
Previous: Image Processing: Flows under
The essential idea in image smoothing is to filter noise present
in the image signal without sacrificing the useful detail. In contrast,
image enhancement focuses on preferentially highlighting certain image
features. Together, they are precursors to many low level vision procedures
such as edge finding [15,5], shape segmentation, and
shape representation [13,14,11].
In this paper, we present a method for image smoothing and enhancement
which is a variant of the
geometric heat equation.
This technique is based on a min/max switch which controls the form of
the application of the geometric heat equation, selecting either flow
by the positive part of the curvature or the negative part, based on a
local decision. This approach has several key virtues.
First, it contains only one enhancement
parameter, which it most cases is automatically chosen. Second,
the scheme automatically picks the stopping criteria;
continued application of the scheme produces no further change.
Third, the method is one of the fastest possible schemes based on
a curvature-controlled approach.
The methods presented in this paper are derived from the
Osher-Sethian [17] level set formulation of front propagation,
which grew out of earlier by Sethian [23] on the mathematical
formulation of curve and surface motion.
The application of this level set perspective to image processing, and
the design of a PDE-based approach to image
enhancement and noise removal was introduced in two pivotal papers;
the work of Alvarez, Lions and Morel [3] and the
work of Osher-Rudin [16]. While the work presented here starts from
the original curve evolution work [23]
and level set formulation presented in [17,24],
it owes a significant debt to the ground-breaking work
of Alvarez, Lions, and Morel and Osher-Rudin.
The fundamental idea in our approach is to return to the simplest
possible problem, namely the evolution of a curve under its curvature.
We design a technique in which the motion of this curve at each
point is based on either 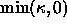 or
or 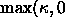 .
This flow stops automatically at a desired point, and forms the core of
our approach. Application of this scheme to both salt-and-pepper
grey-scale noise
and Gaussian noise removal in images is straightforward for binary,
grey-scale, and color images. We then extend the technique to textured
images, making use of both the curvature and the mean curvature
of the underlying image when viewed as a graph.
.
This flow stops automatically at a desired point, and forms the core of
our approach. Application of this scheme to both salt-and-pepper
grey-scale noise
and Gaussian noise removal in images is straightforward for binary,
grey-scale, and color images. We then extend the technique to textured
images, making use of both the curvature and the mean curvature
of the underlying image when viewed as a graph.
The outline of this paper is as follows. First, in Section II, we give a
very brief background. Next, in Section III, we study the motion of a curve
moving under its curvature, and develop an automatic stopping criteria.
In Section IV, we apply this technique to a binary images, and
extend the technique to grey-scale images, textured images, and color
images.



Next: Background
Up: Image Processing: Flows under
Previous: Image Processing: Flows under
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
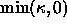 or
or 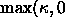 .
This flow stops automatically at a desired point, and forms the core of
our approach. Application of this scheme to both salt-and-pepper
grey-scale noise
and Gaussian noise removal in images is straightforward for binary,
grey-scale, and color images. We then extend the technique to textured
images, making use of both the curvature and the mean curvature
of the underlying image when viewed as a graph.
.
This flow stops automatically at a desired point, and forms the core of
our approach. Application of this scheme to both salt-and-pepper
grey-scale noise
and Gaussian noise removal in images is straightforward for binary,
grey-scale, and color images. We then extend the technique to textured
images, making use of both the curvature and the mean curvature
of the underlying image when viewed as a graph.


