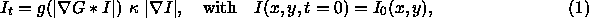
Traditionally, both 1-D and 2-D signals are smoothed by convolving them with a Gaussian kernel; the degree of blurring is controlled by the characteristic width of the Gaussian filter. Since the Gaussian kernel is an isotropic operator, it smooths across the region boundaries thereby compromising their spatial position. As an alternative, Perona and Malik [18] have used an anisotropic diffusion process which performs intraregion smoothing in preference to interregion smoothing. A significant advancement was made by Alvarez, Lions, and Morel (ALM) [3], who presented a comprehensive model for image smoothing.
The ALM model consists of solving an equation of the form
where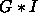 
denotes the image convolved with a Gaussian filter. The geometric
interpretation of the above diffusion equation is that the isointensity
contours of the image move with speed 
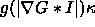, where
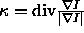is the local curvature. One
variation of this scheme comes from replacing the curvature term with its
affine invariant version (see Sapiro and Tannenbaum [20]).
By flowing the isointensity contours normal to themselves, smoothing
is performed perpendicular to edges thereby retaining edge definition.
At the core of both numerical techniques is
the Osher-Sethian level set algorithm for flowing the isointensity
contours; this technique was also used in related work by Rudin, Osher and
Fatemi [19].
In this work, we return to the original curvature flow equation
and level set algorithm and build a numerical scheme for image
enhancement based on a automatic switch function that controls the motion
of the level
sets in the following way. Diffusion is controlled by
flowing under 
and 
.
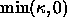The selection between these two types of flows is based on local
intensity and gradient. The resulting technique is an automatic, extremely
robust, computationally efficient, and a straightforward scheme.
To motivate this approach, we begin by discussing curvature motion, namely,
We then develop the complete model which includes image enhancement as well. The crucial ideas on min/max flows upon which this paper is based have been reported earlier by the authors in [10].
