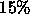 noise means that
at
noise means that
at 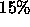 of the pixels, the values in each channel are discarded, and
each is replaced by a random value drawn from a uniform distribution
between 0 and 255.
of the pixels, the values in each channel are discarded, and
each is replaced by a random value drawn from a uniform distribution
between 0 and 255.



The extension of the techniques presented above to color images is straightforward. We decompose the signal into three components (either HSV, RGB, or some other suitable framework), and process each channel separately according to the techniques developed above; the full result is then assembled.
There is a distinct problem with this approach. In each channel, we solve the min/max partial differential equation flow. Because each channel is treated separately, occasionally intermediate values during the flow in each channel can superposition to create a new, unexpected color. This is in fact a well-known problem in color interpolation theory; given any two colors, it is not clear how to smoothly interpolate from one to the other so that the intermediate colors are always perceived as an appropriate blend between the two. While possible solutions are possible if one confines the two colors to restricted regions of color space (such as two colors with the same hue), there is no general solution to this phenomenon. Our algorithm makes no attempt to find an optimal interpolation path through color space; another way to say this is that we do not couple the three distinct partial differential equations.
In Figure 16(a)-(b) we remove noise from a color, textured image of
a rug. Noise is added in all three channels; 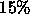 noise means that
at
noise means that
at 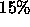 of the pixels, the values in each channel are discarded, and
each is replaced by a random value drawn from a uniform distribution
between 0 and 255.
of the pixels, the values in each channel are discarded, and
each is replaced by a random value drawn from a uniform distribution
between 0 and 255.