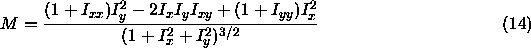
In certain cases, one may want to remove some level of detail in an image; for example, in medical imaging, in which a low level of noise or image gradient is undesired, and the goal is enhancement of features delineated by large gradients. In this case, a simple modification of our min/max flow can achieve good results. We begin by defining the mean curvature of the image when viewed as a graph; that is, let
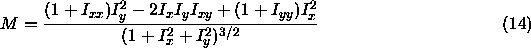
be the mean curvature. If we flow the image according to its mean curvature, i.e.,
this will smooth the image.
Thus, given a user-defined threshold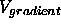 
based on the local
gradient magnitude, we use the following flow to selectively
smooth the image:
Thus, below a prescribed level based on the gradient, we smooth the image
using flow by mean curvature;
above that level, we use our standard min/max flow.
Other choices for the smoothing flow include isotropic diffusion
and curvature flow. We have had the most success with mean curvature flow;
isotropic diffusion is too sensitive to variations in the threshold value
, since edges just below that value are diffused away, while
edges are preserved in mean curvature flow. Our choice of mean curvature
flow over standard curvature flow is because mean curvature flow seems to
perform smoothing in the selected region somewhat faster.
This is an empirical statement rather than one based on a strict proof.
In Figure 11, we show results of this scheme (Eqn.9)
applied to a digital subtraction angiogram (DSA).
In Figure 11a, we show the original image.
In Figure 11b, we show the steady-state min/max flow image.
In Figure 11c, we show the steady-state obtained with
min/max flow coupled to mean curvature flow in the lower gradient range.
We use the value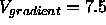 
for this simulation. Derivatives are
computed using central difference approximations with a unit spatial step
size, i.e.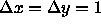 
.
Figure 11: Min/Max Flow with Selective Smoothing. The left image is the
original. The center image is the steady-state of min/max flow. The
right image is the steady-state of the min/max flow together with
mean curvature flow for selective smoothing.
As an experiment, we can apply this min/max flow with an additional
modification to textured images.
Our previous schemes have focussed on viewing the image as
a collection of level curves of the intensity function.
However, viewed as a graph, we may also evaluate the mean curvature
(which is the average of the two principle curvatures) and
the Gaussian curvature (the product of the two principle curvatures) of the
image when viewed as a surface, as discussed
above in the section on selective smoothing.
Viewing a texture as a collection of ridges, valleys, grains, e.t.c.,
in some cases we note that isolated spots of noise (peaks and troughs)
have large absolute values of mean curvature, while the fundamental texture
forms will have, relatively speaking, lower values of the mean curvature.
This is by no means an absolute statement, but suggests an experiment.
We compute the mean curvature of an image when viewed as a graph, and
then establish a lower value (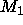
) and an upper value (
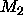) for the
mean curvature.
In the lowest range we turn off all flows; in the middle range we
perform min/max flow, and in the upper range, we perform mean curvature
flow as described above.
We apply the results of this scheme for
processing textured images with noise in Figure 12.
Again, we add salt-and-pepper grey-scale noise to the original. The values of
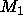and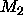 
are set to 2.0 and 3.5 respectively.
Figure 12: Textured Images: Min/Max Flow with Flow Range Determined by
Mean Curvature
