


Next: The Switch Function
Up: Motion of Curves
Previous: The Goal
In this section, we present the switch function to flow the above shape.
Our choice is somewhat mysterious at first; rather than present the reasoning
behind the switch, we shall first describe it, and then in the next section
explain why it works.
Our construction of a switch is motivated by the idea of
comparing the value of a function with its value in a ball around the
function.
Thus, imagine the simplest case, namely
that of a black and white image, in which black is given the value
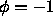 and white given the value
and white given the value 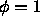 . We select between the two
flows based on the sign of the deviation from the mean value theorem.
Define
. We select between the two
flows based on the sign of the deviation from the mean value theorem.
Define 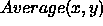 as the average value of the image intensity
as the average value of the image intensity 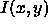 in a
square centered around the point
in a
square centered around the point 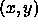 with sidelength
(
with sidelength
(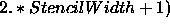 , where, for now StencilWidth=0.
Then, at any point
, where, for now StencilWidth=0.
Then, at any point 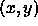 , define the flow by
, define the flow by
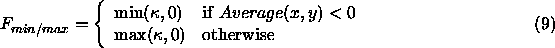
Here, we view 0 as the ``threshold'' value  ; since it is
halfway between the black value of -1 and the white value of 1.
This flow can be seen to thus choose the ``correct'' flow between the min flow
and the max flow.
As a demonstration, in Figure 5a, we show the
initial notched region. In Figure 5b, we show
the results using the min/max given in Eqn. 9.
To verify that our scheme is independent of the positioning of the
colors, we reverse the initial colors and show the results of
the same min/max flow in
Figure 5c.
The small amount of rounding that is seen at the corners is due to
the coarseness of the calculation; the simulation is performed
on a
; since it is
halfway between the black value of -1 and the white value of 1.
This flow can be seen to thus choose the ``correct'' flow between the min flow
and the max flow.
As a demonstration, in Figure 5a, we show the
initial notched region. In Figure 5b, we show
the results using the min/max given in Eqn. 9.
To verify that our scheme is independent of the positioning of the
colors, we reverse the initial colors and show the results of
the same min/max flow in
Figure 5c.
The small amount of rounding that is seen at the corners is due to
the coarseness of the calculation; the simulation is performed
on a 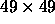 grid, and the contour plotter which locates the zero level
set rounds the edges.
grid, and the contour plotter which locates the zero level
set rounds the edges.

Figure 5: Motion of Notched Region under Min/Max Flow
As a further test, we return to our double-starshaped region, and again
run the min/max flow. We show the initial shape
in Figure 6a. In
Figure 6b, we add an oscillation on the size of
the grid, that is, we alternately switch grid values along the boundary
between the two regions. In Figure 6c,
we then show the results of the min/max flow. What happens is that
the small-scale ``noise'' is removed; once this happens, the boundary
achieves a final state which does not change and preserves structures
larger than the one-pixel wide noise. Thus, the large arms are
not destroyed by the flow.
If we were to exchange the roles of black and white, the same
final shape would be obtained.

Figure 6: Motion of Double-StarShaped Region under Min/Max Flow
We note that the level of noise removed is a function of the size of
the stencil used in computing the switch in the min/max speed.
What remains are structures than are not detected by our threshold stencil.
Thus, the stencil size is the single parameter that determines the flow
and hence the noise removal capabilities.
We view this as a natural and automatic choice of the stencil, since
it is given by the pixel refinement of the image.
However, for a given pixel size, one can choose a larger stencil to
exact noise removal on a larger scale; that is,
we can choose to remove the next larger level
of noise structures by increasing the size of
our threshold stencil by computing the average 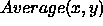 over
a large square.
We then use this larger stencil and continue the process by running
the min/max flow.
We have done this in Figure 7; we start with an
initial shape in Figure 7a which has ``noise'' in the
boundary. We then perform the min/max flow until steady-state is
achieved with stencil size zero in Figure 7b; that is,
the ``average'' consists
only of the value of
over
a large square.
We then use this larger stencil and continue the process by running
the min/max flow.
We have done this in Figure 7; we start with an
initial shape in Figure 7a which has ``noise'' in the
boundary. We then perform the min/max flow until steady-state is
achieved with stencil size zero in Figure 7b; that is,
the ``average'' consists
only of the value of 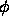 at the point
at the point 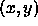 itself.
We note that when we choose a stencil size of zero, nothing happens;
this is explained in detail in the next section.
In Figure 7c, we perform the min/max
flow until steady-state is achieved with stencil size of 1,
and the continue min/max flow with a larger stencil until
steady-state is again achieved in Figure 7d.
As the stencil size is increased, larger and larger structures are
removed.
itself.
We note that when we choose a stencil size of zero, nothing happens;
this is explained in detail in the next section.
In Figure 7c, we perform the min/max
flow until steady-state is achieved with stencil size of 1,
and the continue min/max flow with a larger stencil until
steady-state is again achieved in Figure 7d.
As the stencil size is increased, larger and larger structures are
removed.

Figure 7: Motion of StarShaped Region with Noise under Min/Max Flow at
Various Stencil Levels
We can summarize our results as follows:
- The single min/max flow selects the correct motion to diffuse the
small-scale pixel notches into the boundary.
- The larger, global properties of the shape is maintained.
- Furthermore, and equally importantly, the flow stops once these notches
are diffused into the main structure.
- Edge definition is maintained, and, in some global sense, the
area inside the boundary is roughly preserved up to the order of the
smoothing.
- The noise removal capabilities of the min/max flow is scale-dependent,
and can be hierarchically adjusted.
- The scheme requires only a nearest neighbor stencil evaluation.



Next: The Switch Function
Up: Motion of Curves
Previous: The Goal
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
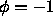 and white given the value
and white given the value 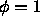 . We select between the two
flows based on the sign of the deviation from the mean value theorem.
Define
. We select between the two
flows based on the sign of the deviation from the mean value theorem.
Define 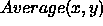 as the average value of the image intensity
as the average value of the image intensity 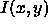 in a
square centered around the point
in a
square centered around the point 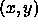 with sidelength
(
with sidelength
(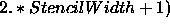 , where, for now StencilWidth=0.
Then, at any point
, where, for now StencilWidth=0.
Then, at any point 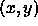 , define the flow by
, define the flow by



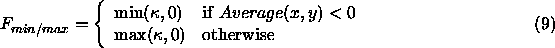
 ; since it is
halfway between the black value of -1 and the white value of 1.
This flow can be seen to thus choose the ``correct'' flow between the min flow
and the max flow.
As a demonstration, in Figure
; since it is
halfway between the black value of -1 and the white value of 1.
This flow can be seen to thus choose the ``correct'' flow between the min flow
and the max flow.
As a demonstration, in Figure 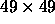 grid, and the contour plotter which locates the zero level
set rounds the edges.
grid, and the contour plotter which locates the zero level
set rounds the edges.


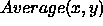 over
a large square.
We then use this larger stencil and continue the process by running
the min/max flow.
We have done this in Figure
over
a large square.
We then use this larger stencil and continue the process by running
the min/max flow.
We have done this in Figure  at the point
at the point 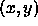 itself.
We note that when we choose a stencil size of zero, nothing happens;
this is explained in detail in the next section.
In Figure
itself.
We note that when we choose a stencil size of zero, nothing happens;
this is explained in detail in the next section.
In Figure 