


Next: The Switch
Up: Motion of Curves
Previous: The Min/Max Flow
Consider now the square with notches on each side shown in
Figure 4a. We imagine that the notches are one unit
wide, where a unit most typically will correspond to a pixel width.
Our goal is to use the above flow to somehow remove the notches which
protrude out from the sides.
In Figure 4b, we see the effect of curvature
flow; the notches are removed, but the shape is fully diffused.
In Figure 4c, we see the effect of
flow with speed 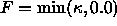 ; here, one set of notches are
removed, but the other set have been replaced by their convex hull.
If we run this flow forever, the figure will not change since the
convex hull has been obtained, which does not move under this flow.
Conversely, as shown in Figure 4d,
obtained with speed
; here, one set of notches are
removed, but the other set have been replaced by their convex hull.
If we run this flow forever, the figure will not change since the
convex hull has been obtained, which does not move under this flow.
Conversely, as shown in Figure 4d,
obtained with speed 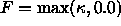 , the inner
notches stay fixed and the front moves in around them, while the
outer notches are diffused. Continual application of this flow causes the
shape to shrink and collapse.
Finally, in Figure 4e and
Figure 4f, we reverse the roles of black and
white, showing the effects of the min and max flows are now reversed.
, the inner
notches stay fixed and the front moves in around them, while the
outer notches are diffused. Continual application of this flow causes the
shape to shrink and collapse.
Finally, in Figure 4e and
Figure 4f, we reverse the roles of black and
white, showing the effects of the min and max flows are now reversed.
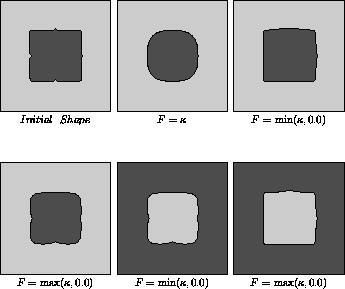
Figure 4: Motion of Notched Region under Various Flows
The problem is that in some places, the notch is ``outwards'', and in
others, the notch is ``inwards''.
Our goal is a flow which somehow chooses the correct choice of flows
between 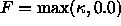 and
and 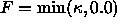 .
The solution lies in a switch function which determines the nature of
the notch.
.
The solution lies in a switch function which determines the nature of
the notch.
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
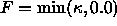 ; here, one set of notches are
removed, but the other set have been replaced by their convex hull.
If we run this flow forever, the figure will not change since the
convex hull has been obtained, which does not move under this flow.
Conversely, as shown in Figure 4d,
obtained with speed
; here, one set of notches are
removed, but the other set have been replaced by their convex hull.
If we run this flow forever, the figure will not change since the
convex hull has been obtained, which does not move under this flow.
Conversely, as shown in Figure 4d,
obtained with speed 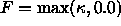 , the inner
notches stay fixed and the front moves in around them, while the
outer notches are diffused. Continual application of this flow causes the
shape to shrink and collapse.
Finally, in Figure 4e and
Figure 4f, we reverse the roles of black and
white, showing the effects of the min and max flows are now reversed.
, the inner
notches stay fixed and the front moves in around them, while the
outer notches are diffused. Continual application of this flow causes the
shape to shrink and collapse.
Finally, in Figure 4e and
Figure 4f, we reverse the roles of black and
white, showing the effects of the min and max flows are now reversed.




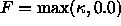 and
and 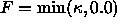 .
The solution lies in a switch function which determines the nature of
the notch.
.
The solution lies in a switch function which determines the nature of
the notch.