


Next: The Goal
Up: Motion of Curves
Previous: Formulation
We now modify the above flow. In order to be careful about signs,
we simply note that the boundary of a disk initialized so that
the inside of the disk corresponds to a negative value for the signed distance
function  and a positive value for the signed distance function
and a positive value for the signed distance function 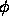 on the outside of the disk has a normal
on the outside of the disk has a normal 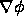 which
points outwards away from the center of the disk, and a curvature
defined as
which
points outwards away from the center of the disk, and a curvature
defined as  which is always
positive on all the convex level contours.
Thus, a flow under speed function
which is always
positive on all the convex level contours.
Thus, a flow under speed function 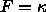 corresponds to the
collapsing curvature flow, since the boundary moves in the direction of
its normal with negative speed, and hence moves inwards.
corresponds to the
collapsing curvature flow, since the boundary moves in the direction of
its normal with negative speed, and hence moves inwards.
We need to be further careful about signs and amend a previous definition.
We shall refer to a speed function F in the context of the level set
equation

thus, from now on, F will give the speed of the front in a direction
opposite to its normal direction. Thus, a curve collapsing under its
curvature will correspond to speed 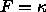 . This will be our
convention for the remainder of this paper.
. This will be our
convention for the remainder of this paper.
Now, motivated by work on
level set methods applied to grid generation [25] and
shape recognition [11], we consider two flows, namely
Here, we have chosen the negative of the signed
distance in the interior, and the positive sign in the
exterior region.
As shown in Figure 2, the effect of flow
under 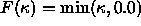 is to allow the inward concave
fingers to grow outwards, while suppressing the motion of the outward
convex regions.
Thus, the motion halts as soon as the convex hull is obtained.
Conversely, the effect of flow under
is to allow the inward concave
fingers to grow outwards, while suppressing the motion of the outward
convex regions.
Thus, the motion halts as soon as the convex hull is obtained.
Conversely, the effect of flow under  is
to allow the outward regions to grow inwards while suppressing the motion of
the inward concave regions. However, once the shape becomes fully convex,
the curvature is always positive and hence the flow becomes the same as
regular curvature flow; hence the shape collapses to a point.
is
to allow the outward regions to grow inwards while suppressing the motion of
the inward concave regions. However, once the shape becomes fully convex,
the curvature is always positive and hence the flow becomes the same as
regular curvature flow; hence the shape collapses to a point.
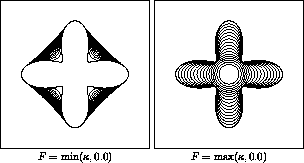
Figure 2: Motion of Curve under Min/Max Flow
We can summarize the above by saying that, for the above case,
flow under 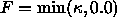 preserves some of the structure of the
curve, while flow under
preserves some of the structure of the
curve, while flow under 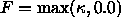 completely diffuses away
all of the information.
completely diffuses away
all of the information.
Before proceeding, we examine a slightly more complex shape, which
is instructive.
In Figure 6, we show what happens to a double
star-shaped region.
We let the color black correspond to the ``inside'' where  and the
white correspond to the ``outside'' where
and the
white correspond to the ``outside'' where 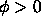 .
First, in Figure 6a,
we show evolution under plain curvature, that is
.
First, in Figure 6a,
we show evolution under plain curvature, that is 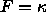 .
Eventually, the shape collapses completely.
In Figure 6b, we show the same curve collapsing
under
.
Eventually, the shape collapses completely.
In Figure 6b, we show the same curve collapsing
under 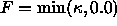 ; here, the outer front
moves to the convex hull, while the inner front collapses and disappears.
The last shown state is stable.
In Figure 6c, we show the same curve collapsing
under
; here, the outer front
moves to the convex hull, while the inner front collapses and disappears.
The last shown state is stable.
In Figure 6c, we show the same curve collapsing
under  ; here, the outer part of the front
collapses, while the inner part expands to its convex hull. Eventually,
the two meet, and the front disappears.
Finally, in Figure 6d, we switch the roles of
black and white; thus flow with speed
; here, the outer part of the front
collapses, while the inner part expands to its convex hull. Eventually,
the two meet, and the front disappears.
Finally, in Figure 6d, we switch the roles of
black and white; thus flow with speed  corresponds
to the same flow as in Figure 6d; changing the
colors corresponds to changing between the maximum flow and the minimum flow.
corresponds
to the same flow as in Figure 6d; changing the
colors corresponds to changing between the maximum flow and the minimum flow.

Figure 3: Motion of Complex Region under Various Flows



Next: The Goal
Up: Motion of Curves
Previous: Formulation
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
 and a positive value for the signed distance function
and a positive value for the signed distance function 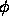 on the outside of the disk has a normal
on the outside of the disk has a normal 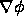 which
points outwards away from the center of the disk, and a curvature
defined as
which
points outwards away from the center of the disk, and a curvature
defined as  which is always
positive on all the convex level contours.
Thus, a flow under speed function
which is always
positive on all the convex level contours.
Thus, a flow under speed function 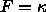 corresponds to the
collapsing curvature flow, since the boundary moves in the direction of
its normal with negative speed, and hence moves inwards.
corresponds to the
collapsing curvature flow, since the boundary moves in the direction of
its normal with negative speed, and hence moves inwards.




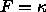 . This will be our
convention for the remainder of this paper.
. This will be our
convention for the remainder of this paper.
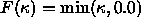

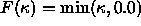 is to allow the inward concave
fingers to grow outwards, while suppressing the motion of the outward
convex regions.
Thus, the motion halts as soon as the convex hull is obtained.
Conversely, the effect of flow under
is to allow the inward concave
fingers to grow outwards, while suppressing the motion of the outward
convex regions.
Thus, the motion halts as soon as the convex hull is obtained.
Conversely, the effect of flow under  is
to allow the outward regions to grow inwards while suppressing the motion of
the inward concave regions. However, once the shape becomes fully convex,
the curvature is always positive and hence the flow becomes the same as
regular curvature flow; hence the shape collapses to a point.
is
to allow the outward regions to grow inwards while suppressing the motion of
the inward concave regions. However, once the shape becomes fully convex,
the curvature is always positive and hence the flow becomes the same as
regular curvature flow; hence the shape collapses to a point.
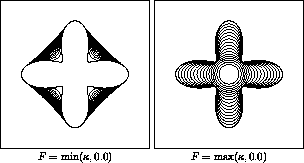
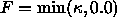 preserves some of the structure of the
curve, while flow under
preserves some of the structure of the
curve, while flow under 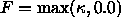 completely diffuses away
all of the information.
completely diffuses away
all of the information.
 and the
white correspond to the ``outside'' where
and the
white correspond to the ``outside'' where 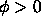 .
First, in Figure
.
First, in Figure 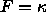 .
Eventually, the shape collapses completely.
In Figure
.
Eventually, the shape collapses completely.
In Figure 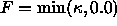 ; here, the outer front
moves to the convex hull, while the inner front collapses and disappears.
The last shown state is stable.
In Figure
; here, the outer front
moves to the convex hull, while the inner front collapses and disappears.
The last shown state is stable.
In Figure  ; here, the outer part of the front
collapses, while the inner part expands to its convex hull. Eventually,
the two meet, and the front disappears.
Finally, in Figure
; here, the outer part of the front
collapses, while the inner part expands to its convex hull. Eventually,
the two meet, and the front disappears.
Finally, in Figure  corresponds
to the same flow as in Figure
corresponds
to the same flow as in Figure 