


Next: The Min/Max Flow
Up: Motion of Curves
Previous: Motion of Curves
Consider a closed, nonintersecting curve in the plane moving
with speed  normal to itself. More precisely,
let
normal to itself. More precisely,
let  be a smooth, closed initial curve
in
be a smooth, closed initial curve
in 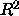 , and let
, and let 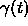 be the one-parameter family of curves
generated by moving
be the one-parameter family of curves
generated by moving 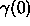 along its normal vector field with
speed
along its normal vector field with
speed 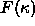 .
Here,
.
Here, 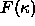 is a given scalar function of the curvature
is a given scalar function of the curvature  .
Thus,
.
Thus, 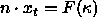 , where x is the position vector of
the curve, t is time, and n is the unit normal to the curve.
, where x is the position vector of
the curve, t is time, and n is the unit normal to the curve.
Consider a speed function of the form 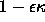 , where
, where  is a constant.
An evolution equation for the curvature
is a constant.
An evolution equation for the curvature  , see [23],
is given by
, see [23],
is given by

where we have taken the second derivative of the curvature  with
respect to arclength
with
respect to arclength 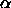 .
This is a reaction-diffusion equation;
the drive toward singularities due to the reaction
term (
.
This is a reaction-diffusion equation;
the drive toward singularities due to the reaction
term (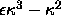 ) is balanced by the smoothing effect of
the diffusion term (
) is balanced by the smoothing effect of
the diffusion term (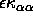 ).
Indeed, with
).
Indeed, with 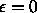 , we have a pure reaction
equation
, we have a pure reaction
equation 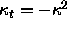 .
In this case, the solution is
.
In this case, the solution is 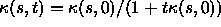 , which
is singular in finite t if the initial curvature is anywhere negative.
Thus, corners can form in the moving curve when
, which
is singular in finite t if the initial curvature is anywhere negative.
Thus, corners can form in the moving curve when 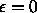 .
.
For  , the front develops a sharp corner
in finite time as discussed above. In general, it is not clear how to
construct the normal at the corner and continue
the evolution, since the derivative is not defined there.
One possibility is the ``swallowtail'' solution formed by letting the
front pass through itself.
However, from a geometrical argument it seems clear that the
front at time t should consist of only the set of all points
located a distance t from the initial curve.
(This is known as the Huyghens principle construction, see [23]).
Roughly speaking, we want to remove the ``tail'' from the ``swallowtail''.
Another way to characterize this weak solution is through the
following ``entropy condition'' posed by Sethian (see [23]):
If the front is viewed as a burning flame,
then once a particle is burnt it stays burnt.
Careful adherence to this stipulation produces the Huyghens principle
construction.
Furthermore, this physically reasonable weak solution
is the formal limit of the smooth solutions
, the front develops a sharp corner
in finite time as discussed above. In general, it is not clear how to
construct the normal at the corner and continue
the evolution, since the derivative is not defined there.
One possibility is the ``swallowtail'' solution formed by letting the
front pass through itself.
However, from a geometrical argument it seems clear that the
front at time t should consist of only the set of all points
located a distance t from the initial curve.
(This is known as the Huyghens principle construction, see [23]).
Roughly speaking, we want to remove the ``tail'' from the ``swallowtail''.
Another way to characterize this weak solution is through the
following ``entropy condition'' posed by Sethian (see [23]):
If the front is viewed as a burning flame,
then once a particle is burnt it stays burnt.
Careful adherence to this stipulation produces the Huyghens principle
construction.
Furthermore, this physically reasonable weak solution
is the formal limit of the smooth solutions 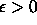 as the curvature
term vanishes, (see [23]).
Extensive discussion of the role
of shocks and rarefactions in propagating fronts may be found
in [22].
as the curvature
term vanishes, (see [23]).
Extensive discussion of the role
of shocks and rarefactions in propagating fronts may be found
in [22].
Let us imagine now a very specific speed function, namely
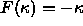 . This case corresponds to a curve collapsing
under its curvature. It can be shown that for an arbitrary smooth
simple curve, (see Gage [8], Grayson [9]), such a curve
collapses to a single point.
In Figure 1a,b, we show a star-shaped region collapsing
under this flow.
. This case corresponds to a curve collapsing
under its curvature. It can be shown that for an arbitrary smooth
simple curve, (see Gage [8], Grayson [9]), such a curve
collapses to a single point.
In Figure 1a,b, we show a star-shaped region collapsing
under this flow.
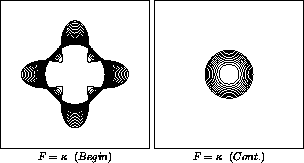
Figure 1: Collapse of Star-Shaped Curve under Curvature
Here, we have evolved the curve using the Osher-Sethian level set
method, see [17]. Briefly, this technique works as follows.
Given a moving closed hypersurface 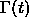 , that is,
, that is,
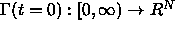 ,
we wish to produce an Eulerian
formulation for the motion of the hypersurface propagating along its
normal direction with speed F, where F can be a function of
various arguments, including the curvature, normal direction, e.t.c.
The main idea is to embed this propagating interface as the
zero level set of a higher dimensional function
,
we wish to produce an Eulerian
formulation for the motion of the hypersurface propagating along its
normal direction with speed F, where F can be a function of
various arguments, including the curvature, normal direction, e.t.c.
The main idea is to embed this propagating interface as the
zero level set of a higher dimensional function 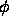 .
Let
.
Let 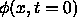 , where
, where  is defined by
is defined by

where d is the distance from x to  , and
the plus (minus) sign is chosen if the point x is outside (inside)
the initial hypersurface
, and
the plus (minus) sign is chosen if the point x is outside (inside)
the initial hypersurface 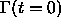 .
Thus, we have an initial function
.
Thus, we have an initial function 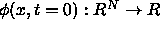 with the property that
with the property that

It can easily be shown that the equation of motion given by


is such that the evolution of the zero level set of  always corresponds
to the motion of the initial hypersurface under the given speed
function F.
This evolution equation Eqn. 7 is solved by means
of difference operators on a fixed Eulerian grid. Care must be taken
in the case where the speed function F contains a hyperbolic
component. For details, see [17,24].
Since its introduction, this approach to front propagation has
been used to model a wide variety of problems, including
the generation of minimal surfaces [6],
fast interface techniques [1],
singularities and geodesics in moving curves and surfaces in [7],
flame propagation [26,27], shape reconstruction
[13,14,12], shape representation and
recognition [11], grid generation [25],
and semiconductor manufacturing [2].
always corresponds
to the motion of the initial hypersurface under the given speed
function F.
This evolution equation Eqn. 7 is solved by means
of difference operators on a fixed Eulerian grid. Care must be taken
in the case where the speed function F contains a hyperbolic
component. For details, see [17,24].
Since its introduction, this approach to front propagation has
been used to model a wide variety of problems, including
the generation of minimal surfaces [6],
fast interface techniques [1],
singularities and geodesics in moving curves and surfaces in [7],
flame propagation [26,27], shape reconstruction
[13,14,12], shape representation and
recognition [11], grid generation [25],
and semiconductor manufacturing [2].



Next: The Min/Max Flow
Up: Motion of Curves
Previous: Motion of Curves
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
 normal to itself. More precisely,
let
normal to itself. More precisely,
let  be a smooth, closed initial curve
in
be a smooth, closed initial curve
in 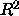 , and let
, and let 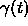 be the one-parameter family of curves
generated by moving
be the one-parameter family of curves
generated by moving 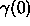 along its normal vector field with
speed
along its normal vector field with
speed 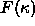 .
Here,
.
Here, 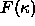 is a given scalar function of the curvature
is a given scalar function of the curvature  .
Thus,
.
Thus, 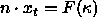 , where x is the position vector of
the curve, t is time, and n is the unit normal to the curve.
, where x is the position vector of
the curve, t is time, and n is the unit normal to the curve.



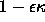 , where
, where  is a constant.
An evolution equation for the curvature
is a constant.
An evolution equation for the curvature  , see [
, see [
 with
respect to arclength
with
respect to arclength 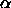 .
This is a reaction-diffusion equation;
the drive toward singularities due to the reaction
term (
.
This is a reaction-diffusion equation;
the drive toward singularities due to the reaction
term (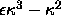 ) is balanced by the smoothing effect of
the diffusion term (
) is balanced by the smoothing effect of
the diffusion term (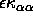 ).
Indeed, with
).
Indeed, with 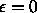 , we have a pure reaction
equation
, we have a pure reaction
equation 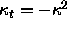 .
In this case, the solution is
.
In this case, the solution is 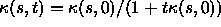 , which
is singular in finite t if the initial curvature is anywhere negative.
Thus, corners can form in the moving curve when
, which
is singular in finite t if the initial curvature is anywhere negative.
Thus, corners can form in the moving curve when 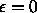 .
.
 , the front develops a sharp corner
in finite time as discussed above. In general, it is not clear how to
construct the normal at the corner and continue
the evolution, since the derivative is not defined there.
One possibility is the ``swallowtail'' solution formed by letting the
front pass through itself.
However, from a geometrical argument it seems clear that the
front at time t should consist of only the set of all points
located a distance t from the initial curve.
(This is known as the Huyghens principle construction, see [
, the front develops a sharp corner
in finite time as discussed above. In general, it is not clear how to
construct the normal at the corner and continue
the evolution, since the derivative is not defined there.
One possibility is the ``swallowtail'' solution formed by letting the
front pass through itself.
However, from a geometrical argument it seems clear that the
front at time t should consist of only the set of all points
located a distance t from the initial curve.
(This is known as the Huyghens principle construction, see [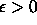 as the curvature
term vanishes, (see [
as the curvature
term vanishes, (see [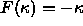 . This case corresponds to a curve collapsing
under its curvature. It can be shown that for an arbitrary smooth
simple curve, (see Gage [
. This case corresponds to a curve collapsing
under its curvature. It can be shown that for an arbitrary smooth
simple curve, (see Gage [
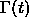 , that is,
, that is,
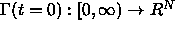 ,
we wish to produce an Eulerian
formulation for the motion of the hypersurface propagating along its
normal direction with speed F, where F can be a function of
various arguments, including the curvature, normal direction, e.t.c.
The main idea is to embed this propagating interface as the
zero level set of a higher dimensional function
,
we wish to produce an Eulerian
formulation for the motion of the hypersurface propagating along its
normal direction with speed F, where F can be a function of
various arguments, including the curvature, normal direction, e.t.c.
The main idea is to embed this propagating interface as the
zero level set of a higher dimensional function 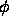 .
Let
.
Let 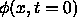 , where
, where  is defined by
is defined by

 , and
the plus (minus) sign is chosen if the point x is outside (inside)
the initial hypersurface
, and
the plus (minus) sign is chosen if the point x is outside (inside)
the initial hypersurface 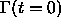 .
Thus, we have an initial function
.
Thus, we have an initial function 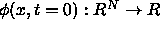 with the property that
with the property that



 always corresponds
to the motion of the initial hypersurface under the given speed
function F.
This evolution equation Eqn.
always corresponds
to the motion of the initial hypersurface under the given speed
function F.
This evolution equation Eqn.