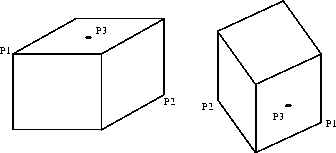
Figure 1: Corresponding points on a cube
Figure 1, below, illustrates the basic problem. We wish to estimate the pose of the cube on the right with respect to the cube on the left. In general, 3 non-collinear points which correspond are sufficient to define an exact solution.
Figure 1: Corresponding points on a cube
Assume the set of points in the model space is
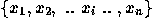
and the corresponding set of points in the scene space is
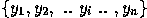
Assuming the points correspond, then each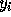 
is obtained by the rotation and translation of each 
.
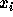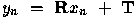
Instead of points, other corresponding primitives may be used, for example a point and two vectors should determine a unique pose. Considering the stated application, we can define points as space curve intersections (e.g. the cube corners ), as centroids of surfaces ( e.g. the centre of a sphere or the centre of a planar patch ) and so on. Vectors could be defined as the normals to planar patches, the axes of cylinders and so on.
In general, a model will have a large number of such ``control points''. Similarly, a segmented depth image will have several surface patches, say, and several scene points and vectors which could be used to deduce pose, assuming they have corresponding model points and vectors. We could use subsets of three points to generate pose hypotheses, and then attempt to verify each hypothesis by searching for other correspondences. Alternatively, we could use all the corresponding points ( or points which we assume to correspond ) to determine the best pose. In general, there will be errors in the scene description, so an exact solution will not be found. Then we can obtain a least square estimate, i.e. one which minimises the residual error between the transformed model, say, and the scene data control points. ( This method has the usual problem of least squares methods, i.e. it does not cope well with outliers, so may have to be modified to include a robust fit in specific cases ).
