From equations 1, 2 and 3 the 3D-3D pose estimation problem is to infer R and T from the sets of corresponding points. Expressed as a least squares problem, we wish to minimise,
To simplify this problem, we can compute the mean values (centroids) of each set of points, and translate them in space so that these lie at the origin. Then compute R, such that
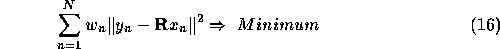
To minimise this function, we first expand the left hand side of
Equation 15. This requires some matrix algebra (See ref. 2,Kanatani, 93, pages 21, 106, 118, 133). For two matrices,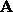 
and 
,
.
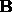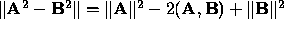The notation,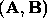 
denotes the Euclidean inner product
of vectors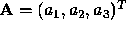 
and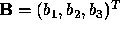 
which is equal to 
.
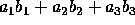Further,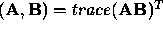 
.
Re-examining equation 18, above, the first and third terms are fixed depending on the weighting function and the point sets. Hence we wish to maximise the second term in order to minimise the whole expression. In other words,
is the correlation matrix
Hence the problem can now be stated. Compute a rotation matrix, R, so that
Solutions to this problem can be found based on singular value decomposition, polar value decomposition or quaternions (See references Haralick et al, 1989, and Kanatani, 1993.) Based on singular value decomposition, we decompose the correlation matrix, K into the form
where
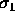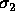and 
, 
and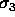 
are the singular values.
The rank of K is
equal to the number of linearly independent columns or rows of K.
Since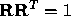 
, Equation 19, above, is maximised if,
This gives a unique solution for the rotation matrix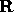 
provided
the rank of 
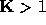and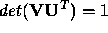 
, or if
the rank of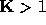 
and the minimum singular value is a
simple root.
Finally, the translation vector, 
is defined
[ Pose Estimation: Contents |
Examples of 3D-3D pose estimation ]
