

First, define a pyramid illustrated in Figure 3, below, by the five vertex points
x = ((1,1,0),(1,-1,0),(-1,-1,0),(-1,1,0),( 0,0,1))
Then consider a rotation of 45 degrees about the axis,
Rotation of the pyramid using the rotation matrix defined above gives
the vertex coordinates,
Then we can translate the rotated pyramid by a translation vector
(1,2,3) to give a new pts list, also illustrated in Figure 4.
Then, we can add random errors to the list of scene points,
and translation vector, (1.056,2.05,3.03), with a mean square
residual error
between the rotated model and scene data of (0.004,0.032,0.009).
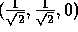 . Using
Equation 12 the rotation matrix is (to two
decimal places )
. Using
Equation 12 the rotation matrix is (to two
decimal places )
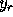 = ((1,1,0),(0.71,-0.71,-1),(-1,-1,0),(-0.71,0.71,1),(0.50,-0.50,0.71)
The resultant pyramid is illustrated in Figure 4, below.
= ((1,1,0),(0.71,-0.71,-1),(-1,-1,0),(-0.71,0.71,1),(0.50,-0.50,0.71)
The resultant pyramid is illustrated in Figure 4, below.
 = ((2,3,3),(1.71,1.29,2),(0,1,3),(0.29,2.71,4),(1.50,1.50,3.71))
Then we can use the Least Squares technique to calculate the rotation
matrix, given the control points which define the vertices in
Figures 3 and 4. This recovers the original
rotation matrix Equation 26, above) and translation defined
above with no residual error.
= ((2,3,3),(1.71,1.29,2),(0,1,3),(0.29,2.71,4),(1.50,1.50,3.71))
Then we can use the Least Squares technique to calculate the rotation
matrix, given the control points which define the vertices in
Figures 3 and 4. This recovers the original
rotation matrix Equation 26, above) and translation defined
above with no residual error.
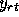 , for example,
, for example,
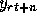 = (2.10,3.05,3.20),(1.77,1.28,2.05),(0.02,1.00,2.87),(0.29,2.91,3.99),(1.51,1.48,3.78))
When the pose estimate is recomputed, we now obtain a different rotation matrix,
a different translation vector, and a finite residual error.
= (2.10,3.05,3.20),(1.77,1.28,2.05),(0.02,1.00,2.87),(0.29,2.91,3.99),(1.51,1.48,3.78))
When the pose estimate is recomputed, we now obtain a different rotation matrix,
a different translation vector, and a finite residual error.



[ Pose Estimation: Contents |
Matching a model to depth data ]