Basic Considerations

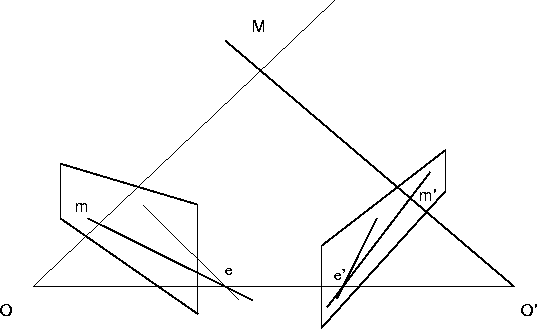
Consider the case of two perspective images of a rigid scene. The geometry of the configuration is depicted in fig. 5.1. The 3D point M projects to point m in the left image and m' in the right one.

  

Figure 5.1: Epipolar geometry

Let O and O' be the centres of projection of the left and right camera respectively. The M's epipolar plane [O, O', M]intersects the image planes in two conjugate lines called M's epipolar lines. These pass respectively through the images m and m' and the points e and e' of intersection of the image planes with the base line [O, O']. These conjugate points are called the epipoles of the stereo rig.

Now let M move around in space. The epipolar planes form a pencil of planes through [O,O'], and the epipolar lines form two pencils of lines through e and e' respectively.

Key Property: The epipolar line-line and line-plane correspondences are projective.

Proof: Perspective projection through any third point on [O,O']provides the required projective collineation. $\sqcup \!\!\!\! \sqcap$

Projectively, the epipolar geometry is all there is to know about a stereo rig. It establishes the correspondence $m \leftrightarrow m'$, and allows 3D reconstruction of the scene to be carried out up to an overall 3D projective deformation (which is all that can be done with any number of completely uncalibrated cameras, without further constraints). An important practical application of epipolar geometry is to aid the search for corresponding points, reducing it from the entire second image to a single epipolar line. The epipolar geometry is sometimes obtained by calibrating each of the cameras with respect to the same 3D frame, but as the next section shows, it can easily be found from a few point correspondences, without previous camera calibration.