 |
We have not implemented the specific suggestions of section 4.2 for the recovery of Euclidean structure from a projective reconstruction by observing known scene angles, circles,...However we have developed a more brute force approach, finding a projective transformation H in equation (5.4) that maps the projective reconstruction to one that satisfies a set of redundant Euclidean constraints. This simultaneously minimizes the error in the projection equations and the violation of the constraints. The equations are highly nonlinear and a good initial guess for the structure is needed. In our experiments this was obtained by assuming parallel projection, which is linear and allows easy reconstruction using SVD decomposition ([26]).
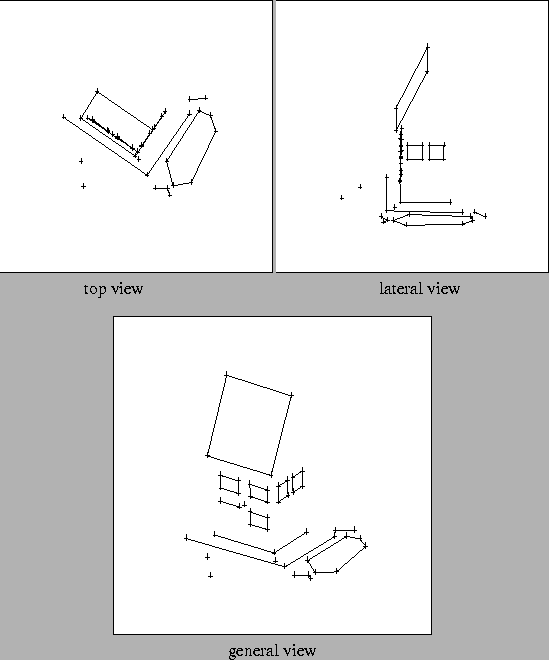
Figures 5.3 and 5.4 show an example of this
process.
 |
 |