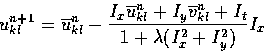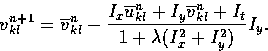

Next: References
Up: Computer Vision IT412
Previous: Structure from motion
Optical flow techniques are based on the idea that for most
points in the image, neighbouring points have approximately the
same brightness. In other words, the world is made up of continuous
objects over which brightness varies smoothly.
Let I(x,y,t) be the irradiance at time t at the image
point (x,y). If a little patch of uniform brightness around
(x,y) does not change with time, then
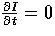 , implying
, implying
Ix dx/dt + Iy dy/dt + It = 0.
Now let u = dx/dt and v = dy/dt. Using the values of u and v
at a grid point (i,j) and its neighbours, we can measure a departure
from smoothness by
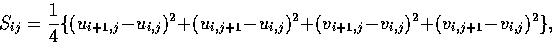
while any error in the optical flow constraint equation is given by
Cij = (Ixui,j + Iyvi,j + It)2.
So we want a set of values ui,j and vi,j that minimize
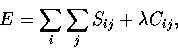
where 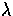 is a regularisation constant.
is a regularisation constant.
We differentiate E with respect to ukl and vkl to get
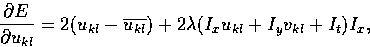
and
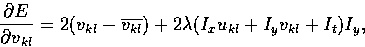
where 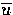 and
and 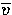 are local averages of u and v.
are local averages of u and v.
We equate these expressions to zero to get
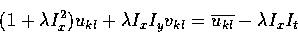
and
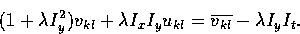
This gives us two equations in the two unknowns ukl and vkl.
These can be solved directly and suggest the iterative scheme
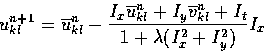
and
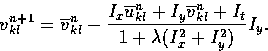
In other words, the new value of (u,v) at a point is equal to the average
of the surrounding values minus an adjustment in the direction
of the brightness gradient.
Note that this scheme also requires estimates of the values Ix, Iy
and It. These can be computed by taking local averages in neighbourhoods
about the grid point (i,j,k).


Next: References
Up: Computer Vision IT412
Previous: Structure from motion
Robyn Owens
10/29/1997
![]() , implying
, implying
![]()
![]()
![]()
![]()
![]()
![]()