Measurements and Noise

No imaging system is perfect. Noise is introduced into the imaging process via the use of real lenses and cameras that differ in operation from the pinhole camera model. Moreover, lighting and atmospheric conditions can also effect the resulting image. In addition, digital images suffer deviations in image values introduced by sampling. Thus, measurements are affected by fluctuations in the signal being measured, and these fluctuations are described according to some probability distribution, p(x).

Since p(x) is a probability distribution, it always satisfies

$$p(x)\geq 0, \mbox{for all $x$}$$

and

$$\int_{-\infty}^{\infty} p(x)dx = 1.$$

The mean or first moment of the distribution $\mu$ is given by

$$\mu = \frac{ \int_{-\infty}^{\infty} x p(x) dx} { \int_{-\infty}^{\infty} p(x)dx},$$

but

$$\int_{-\infty}^{\infty} p(x) dx = 1,$$

implying

$$\mu = \int_{-\infty}^{\infty} x p(x)dx.$$

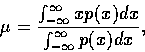
The spread of the distribution is given by the second moment or variance:

$${\rm variance = (std. deviation)}^{2} = \sigma^2 = \int_{-\infty}^{\infty}(x-\mu)^2 p(x)dx.$$

The cumulative probability distribution

$$P(x) = \int_{-\infty}^{x} p(t) dt$$

tells us the probability that the measurement will be less than or equal to x. Thus, the probability density distribution is just the derivative of the cumulative probability distribution, that is, p(x) = P'(x).

One way to improve accuracy is to average several measurements, assuming that the `noise' in them will be independent and tend to cancel out. To see how this is indeed the case, we consider the following analysis.

Let x = x₁+x₂, the sum of two independent variables with probability distributions p₁(x₁) and p₂(x₂). Then what can we say about p(x), the probability distribution of x?

We first look at the probability of getting a value between x and $x +\delta x$. If the sum x₁ + x₂ is between x and $x +\delta x$,and we are given a value of x₂, then x₁ must be between x-x₂ and $x + \delta x-x_{2}$. The probability of this occurring is $p_{1}(x-x_{2})\delta x$.

But x₂ can also take on a range of values. The probability that x₂ lies between a particular x₂ and $x_{2} + \delta x_{2}$ is

$$p_{2}(x_{2})\delta x_{2}.$$

To get the probability that the sum lies between x and $x +\delta x$ we have to integrate the product over all x₂. Thus

$$p(x) \delta{x} = \int_{-\infty}^{\infty} p_{1}(x - x_{2}) \delta x p_{2}(x_{2}) dx_{2},$$

or

$$p(x) = \int_{-\infty}^{\infty}p_{1}(x - t) p_{2}(t) dt,$$

where t is a dummy variable of integration.

By a similar argument we can show symmetrically that

$$p(x) = \int_{-\infty}^{\infty}p_{2}(x - t) p_{1}(t) dt.$$

This is called the convolution of p₁ and p₂ and is denoted by $p_{1} \otimes p_{2}$.

We can use this result to prove that the mean of the sum of several random variables is equal to the sum of the means, and the variance of the sum is the sum of the variances.

Taking multiple measurements of a variable

If we calculate the average of N independent measurements each having mean $\mu$ and standard deviation $\sigma$, then

$$\overline{x} = \frac{1}{N} \sum{x_{i}}.$$

So the average $\overline{x}$ will have mean $\mu$ $= \frac{1}{N} N \mu$and standard deviation $\frac{\sigma}{\sqrt{N}}$.

This latter result is because the variance of the sum of the distributions is just $N \sigma^{2}$, and so the standard deviation of the sum is $\sqrt{N} \sigma$. Thus the distribution $\overline{x}$ has standard deviation $\frac{\sigma}{\sqrt{N}}$ and hence we obtain a more accurate measurement by taking the average of N independent measurements.

The usual probability distribution we use to model noise in an image is the normal or Gaussian distribution with mean $\mu$ and standard deviation $\sigma$ given by

$$p(x) = \frac{1}{\sqrt{2 \pi \sigma}} e^{-\frac{1}{2}(\frac{x -\mu}{\sigma})^{2}}.$$

Of course, digital images are sampled versions of continuous or analog images, and the sampling is done both spatially and in the luminance values (where it is known as quantization).