Let us take into consideration the definition of Fourier transform in the continuous domain first: Under certain conditions upon the function p(t) the Fourier transform of this function exists and can be defined as
where 
and f is a temporal frequency. With the inverse Fourier transform, the original signal is given by:
Let us take into consideration now the case of the discrete Fourier transform (DFT). In this case we have a finite number N of samples of the signal p(t) taken at regular intervals of duration 
(which can be considered a sampling interval). In practical cases the signal p(t) has not an infinite duration, but its total duration is 
and we have a set 
of samples of the signal p(t) taken at regular intervals. We can define 
, where 
, for 
, is the sampling coordinate.
In the case of the discrete Fourier transform, not only we want the signal to be discrete and not continuous, but we also want the Fourier transform, which is a function of the temporal frequency, to be defined only at regular points of the frequency domain. That is to say that the function 
is not defined for every value of 
but only for certain values 
. We want the samples 
to be regularly spaced as well, so that all the samples are multiples of a dominant frequency 
, that is to say 
, for 
. Let us note now that T is equal to the finite duration of the signal p(x) from which we want to define its discrete Fourier transform. Note also that we assume the number of samples in frequency to be equal to the number of samples in the temporal domain, that is N. This is not a necessary condition, but it simplifies the notation.
All that said, the direct extension of Definition (1) to the discrete domain is:
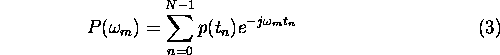
Considering that can assume only discrete values 
and 
can assume only discrete values 
, it is possible to rewrite Definition (3) as:
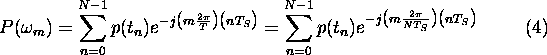
It is now possible to simplify and express the dependence on only in terms of m and the dependence on only in terms of n. In that way the final definition of the DFT is:
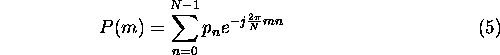
And the inverse of the discrete Fourier transform (IDFT) as:
