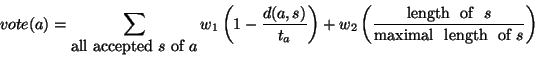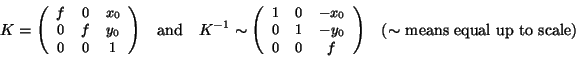Next: Results
Up: A vanishing point detection
Previous: A vanishing point detection
Accumulation Step
Due to various reasons is the perspective projection of a line segment
from the 3D scene onto the 2D image not congruent with the line segment
detected in the image. We denote this perfect projection of a line
segment as projected line segment. Hence, all vanishing points
detection methods have to formulate either implicitly or explicitly a
distance function between a vanishing point and a detected line
segment. In this context the basic question is: How close is a
projected line segment 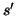 with vanishing point
with vanishing point 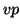 to its
corresponding line segment
to its
corresponding line segment 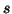 .
In order to answer the question we represent a line segment with
the midpoint representation
.
In order to answer the question we represent a line segment with
the midpoint representation
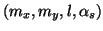 (see figure 3).
We define: The perfect line segment
(see figure 3).
We define: The perfect line segment 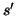 of a line segment
of a line segment 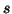 has the
same midpoint as
has the
same midpoint as 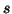 and has
and has 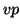 as vanishing point.
On the basis of this definition a distance function
as vanishing point.
On the basis of this definition a distance function 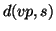 between a
vanishing point
between a
vanishing point 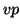 and a line segment
and a line segment 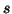 can be defined as the
angle
can be defined as the
angle 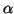 between the corresponding line segments
between the corresponding line segments 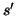 and
and 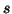 .
Figure 3 gives an example for a finite vanishing point.
This distance function fulfill the requirements:
Finite and infinite vanishing points are treated in the same way and the
distances between points and line segments are independent of
their location on the image plane.
.
Figure 3 gives an example for a finite vanishing point.
This distance function fulfill the requirements:
Finite and infinite vanishing points are treated in the same way and the
distances between points and line segments are independent of
their location on the image plane.
Figure 3:
Explanation for the distance
function 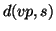 between a line segment
between a line segment 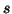 and a finite vanishing point
and a finite vanishing point 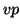 .
.
|
|
We are now able to formulate and fill the
accumulator space. The intersection
points, perhaps at infinity, of all pairs of non-collinear line segments
are considered as accumulator cells, i.e. potential vanishing
points. A line segment 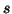 votes for an accumulator cell
votes for an accumulator cell 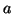 if the distance
if the distance
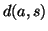 is below a certain threshold
is below a certain threshold 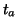 and the vanishing
point does not lie on the projected line segment
and the vanishing
point does not lie on the projected line segment 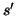 , which correspond to
, which correspond to 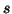 .
In the search step we are interested in the total vote of an accumulator
cell. This vote depends on the length of a line segment (assuming
that longer line segments are more reliable)
as well as on the distance between accepted line segments and the
accumulator cell.
We define
.
In the search step we are interested in the total vote of an accumulator
cell. This vote depends on the length of a line segment (assuming
that longer line segments are more reliable)
as well as on the distance between accepted line segments and the
accumulator cell.
We define
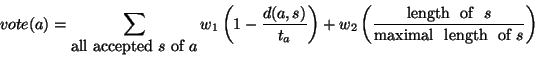 |
(1) |
as the total vote of an accumulator cell 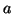 , where
the weights
, where
the weights 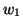 and
and 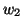 establish this trade off.
establish this trade off.
Search Step
Vanishing points which correspond to mutual
orthogonal directions in the scene have to fulfill the following three
criteria: Orthogonal criterion, camera criterion and vanishing line
criterion.
The first two criteria are affiliated with each other and we consider them
first.
Let us consider a special type of perspective cameras with
zero skew and same scale factor horizontally and vertically (aspect
ratio one). This means that the intrinsic camera matrix is:
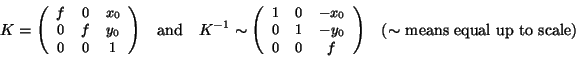 |
(2) |
with the focal length 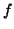 and the principle
point
and the principle
point
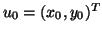 .
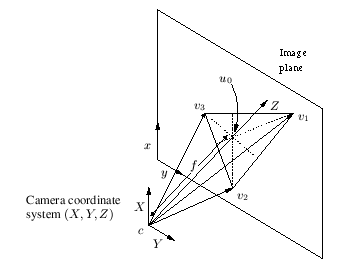
We denote the three vanishing points on the image plane by
.
We denote the three vanishing points on the image plane by 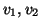 and
and 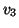 . Since the vector
. Since the vector 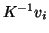 from the camera centre
from the camera centre 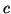 to the vanishing point
to the vanishing point 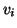 has the
vanishing point
has the
vanishing point 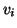 (see figure 4),
we can formulate the orthogonal criterion as:
(see figure 4),
we can formulate the orthogonal criterion as:
where
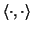 is the scalar product.
In order to determine the vector
is the scalar product.
In order to determine the vector 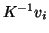 the focal length and the
principle point have to be determined.
the focal length and the
principle point have to be determined.
Figure 4:
Explanation for the camera geometry and
the orthogonal criterion.
|
|
It has been shown [4,9,16] that this can
be achieved if all vanishing points are finite.
Figure 4 shows such a case.
The intersection point of the heights of the triangle
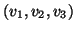 defines the
principle point and the size of this triangle fixes the focal length.
However, in the case of one vanishing point at infinity
the principle point is not defined uniquely. It lies on the line segment, which is defined
by the two endpoints
defines the
principle point and the size of this triangle fixes the focal length.
However, in the case of one vanishing point at infinity
the principle point is not defined uniquely. It lies on the line segment, which is defined
by the two endpoints 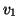 and
and  .
Since the principle point is more likely positioned in the centre of
the image, we choose it as the point, which lies
on the line segment and is closest to the midpoint of the image.
If two vanishing points are at infinity, the focal length can not be
determined. However, the orthogonal criterion can still be checked
since
.
Since the principle point is more likely positioned in the centre of
the image, we choose it as the point, which lies
on the line segment and is closest to the midpoint of the image.
If two vanishing points are at infinity, the focal length can not be
determined. However, the orthogonal criterion can still be checked
since
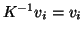 if
if 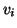 is at infinity, i.e.
is at infinity, i.e.
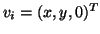 (see equation 2).
We can now specify the camera criterion. This criterion is fulfilled
when the principle point and the focal length are inside a
certain range, in the case they are calculable.
Note, the additional check of the orthogonal criterion is needed
for the case of one or two vanishing points at infinity.
(see equation 2).
We can now specify the camera criterion. This criterion is fulfilled
when the principle point and the focal length are inside a
certain range, in the case they are calculable.
Note, the additional check of the orthogonal criterion is needed
for the case of one or two vanishing points at infinity.
Let us consider the vanishing line criterion.
Two vanishing points 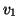 and
and  have a vanishing line when not both vanishing
points are at infinity (see figure 1). This
criterion checks that a line segment which votes for two vanishing points
have a vanishing line when not both vanishing
points are at infinity (see figure 1). This
criterion checks that a line segment which votes for two vanishing points 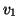 and
and  is close to the vanishing line of
is close to the vanishing line of 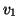 and
and  (see
[13] for a formal definition of the criterion).
(see
[13] for a formal definition of the criterion).
Algorithm
A brute force version for vanishing point detection is:
The Accumulation Step:
Establish the accumulator space (intersection of all pairs of non-collinear line segments)
Determine the vote of each accumulator cell (equation 1)
The Search Step:
Take the accumulator cell 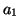 with the highest vote
with the highest vote
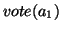 (equation 1)
(equation 1)
Go through all pairs of accumulator cells 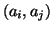
 If the vanishing line criterion is fulfilled for
If the vanishing line criterion is fulfilled for 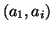 ,
, 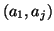 and
and 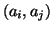
 If the orthogonal criterion and camera criterion is fulfilled for
If the orthogonal criterion and camera criterion is fulfilled for
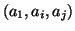
 Calculate
Calculate
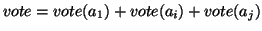
Take the accumulator cells 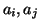 , with the highest vote
, with the highest vote 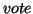
The vanishing points which correspond to the accumulator cells 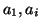 and
and 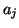 represent the three mutual orthogonal directions of
the scene.
represent the three mutual orthogonal directions of
the scene.



Next: Results
Up: A vanishing point detection
Previous: A vanishing point detection
Carsten Rother
2001-09-14
![\includegraphics[width=7cm]{metric_img.eps}](img16.gif)