 Measurement
Geometries
Measurement
Geometries
Solid Angles
One of the key concepts to understanding the relationships between measurement
geometries is that of the solid angle, or steradian. A sphere contains
4p steradians. A steradian is defined
as the solid angle which, having its vertex at the center of the sphere,
cuts off a spherical surface area equal to the square of the radius of
the sphere. For example, a one steradian section of a one meter radius
sphere subtends a spherical surface area of one square meter.
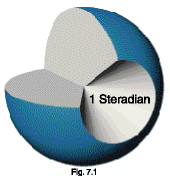 The sphere shown in cross section in figure 7.1 illustrates the concept.
A cone with a solid angle of one steradian has been removed from the sphere.
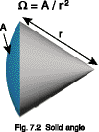
This removed cone is shown in figure 7.2. The solid angle, W,
in steradians, is equal to the spherical surface area, A, divided by the
square of the radius, r.
The sphere shown in cross section in figure 7.1 illustrates the concept.
A cone with a solid angle of one steradian has been removed from the sphere.
This removed cone is shown in figure 7.2. The solid angle, W,
in steradians, is equal to the spherical surface area, A, divided by the
square of the radius, r.
Most radiometric measurements do not require an accurate calculation
of the spherical surface area to convert between units. Flat area
estimates can be substituted for spherical area when the solid angle is
less than 0.03 steradians, resulting in an error of less than one percent.
This roughly translates to a distance at least 5 times greater than the
largest dimension of the detector. In general, if you follow the
ďfive times ruleĒ for approximating a point source,
you can safely estimate using planar surface area.
Radiant and Luminous Flux
 Radiant flux is a measure of radiometric power. Flux, expressed in
watts, is a measure of the rate of energy flow, in joules per second.
Since photon energy is inversely proportional to wavelength, ultraviolet
photons are more powerful than visible or infrared.
Radiant flux is a measure of radiometric power. Flux, expressed in
watts, is a measure of the rate of energy flow, in joules per second.
Since photon energy is inversely proportional to wavelength, ultraviolet
photons are more powerful than visible or infrared.
Luminous flux is a measure of the power of visible light. Photopic
flux, expressed in lumens, is weighted to match the responsivity of the
human eye, which is most sensitive to yellow-green. Scotopic flux
is weighted to the sensitivity of the human eye in the dark adapted state.
Units Conversion: Power
RADIANT FLUX:
1 W (watt)
= 683.0 lm at 555 nm
= 1700.0 scotopic lm at 507 nm
1 J (joule)
= 1 W*s (watt * second)
= 107 erg
= 0.2388 gram * calories
LUMINOUS FLUX:
1 lm (lumen)
= 1.464 x 10-3 W at 555 nm
= 1/(4p) candela (only if isotropic)
1 lm*s (lumen * seconds)
= 1 talbot (T)
= 1.464 x 10-3 joules at 555 nm
l
nm |
Photopic
Luminous
Efficiency |
Photopic
lm / W
Conversion |
Scotopic
Luminous
Efficiency |
Scotopic
lm / W
Conversion |
380
390
400
410
420
430
440
450
460
470
480
490
500
507
510
520
530
540
550
555
560
570
580
590
600
610
620
630
640
650
660
670
680
690
700
710
720
730
740
750
760
770 |
0.000039
.000120
.000396
.001210
.004000
.011600
.023000
.038000
.060000
.090980
.139020
.208020
.323000
.444310
.503000
.710000
.862000
.954000
.994950
1.000000
.995000
.952000
.870000
.757000
.631000
.503000
.381000
.265000
.175000
.107000
.061000
.032000
.017000
.008210
.004102
.002091
.001047
.000520
.000249
.000120
.000060
.000030 |
0.027
0.082
0.270
0.826
2.732
7.923
15.709
25.954
40.980
62.139
94.951
142.078
220.609
303.464
343.549
484.930
588.746
651.582
679.551
683.000
679.585
650.216
594.210
517.031
430.973
343.549
260.223
180.995
119.525
73.081
41.663
21.856
11.611
5.607
2.802
1.428
0.715
0.355
0.170
0.082
0.041
0.020 |
0.000589
.002209
.009290
.034840
.096600
.199800
.328100
.455000
.567000
.676000
.793000
.904000
.982000
1.000000
.997000
.935000
.811000
.650000
.481000
.402000
.328800
.207600
.121200
.065500
.033150
.015930
.007370
.003335
.001497
.000677
.000313
.000148
.000072
.000035
.000018
.000009
.000005
.000003
.000001
.000001 |
1.001
3.755
15.793
59.228
164.220
339.660
557.770
773.500
963.900
1149.200
1348.100
1536.800
1669.400
1700.000
1694.900
1589.500
1378.700
1105.000
817.700
683.000
558.960
352.920
206.040
111.350
56.355
27.081
12.529
5.670
2.545
1.151
0.532
0.252
0.122
.060
.030
.016
.008
.004
.002
.001 |
Irradiance and Illuminance:
Irradiance is a measure of radiometric flux per unit area, or flux density.
Irradiance is typically expressed in W/cm2 (watts per square
centimeter) or W/m2 (watts per square meter).
Illuminance is a measure of photometric flux per unit area, or visible
flux density. Illuminance is typically expressed in lux (lumens per
square meter) or foot-candles (lumens per square foot).
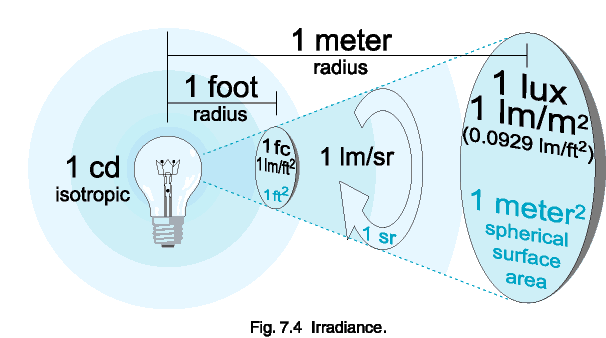 In figure 7.4, above, the lightbulb is producing 1 candela. The candela
is the base unit in light measurement, and is defined as follows:
a 1 candela light source emits 1 lumen per steradian in all directions
(isotropically). A steradian is defined as the solid angle which,
having its vertex at the center of the sphere, cuts off an area equal to
the square of its radius. The number of steradians in a beam is equal
to the projected area divided by the square of the distance.
In figure 7.4, above, the lightbulb is producing 1 candela. The candela
is the base unit in light measurement, and is defined as follows:
a 1 candela light source emits 1 lumen per steradian in all directions
(isotropically). A steradian is defined as the solid angle which,
having its vertex at the center of the sphere, cuts off an area equal to
the square of its radius. The number of steradians in a beam is equal
to the projected area divided by the square of the distance.
So, 1 steradian has a projected area of 1 square meter at a distance
of 1 meter. Therefore, a 1 candela (1 lm/sr) light source will similarly
produce 1 lumen per square foot at a distance of 1 foot, and 1 lumen per
square meter at 1 meter. Note that as the beam of light projects farther
from the source, it expands, becoming less dense. In fig. 7.4, for example,
the light expanded from 1 lm/ft2 at 1 foot to 0.0929 lm/ft2
(1 lux) at 3.28 feet (1 m).
Cosine Law
Irradiance measurements should be made facing the source, if possible.
The irradiance will vary with respect to the cosine of the angle between
the optical axis and the normal to the detector.
Calculating Source Distance
Lenses will distort the position of a point source. You can solve
for the virtual origin of a source by measuring irradiance at two points
and solving for the offset distance, X, using the Inverse Square Law:
E1(d1 + X)2 =
E2(d2 + X)2
Figure 7.5 illustrates a typical setup to determine the location of
an LEDís virtual point source (which is behind the LED due to the built-in
lens). Two irradiance measurements at known distances from a reference
point are all that is needed to calculate the offset to the virtual point
source.

Units Conversion: Flux Density
1 W/cm2 (watts per square centimeter)
= 104 W/m2 (watts per square meter)
= 6.83 x 106 lux at 555 nm
= 14.33 gram*calories/cm2/minute
ILLUMINANCE:
1 lm/m2 (lumens per square meter)
= 1 lux (lx)
= 10-4 lm/cm2
= 10-4 phot (ph)
= 9.290 x 10-2 lm/ft2
= 9.290 x 10-2 foot-candles (fc)
Radiance and Luminance:
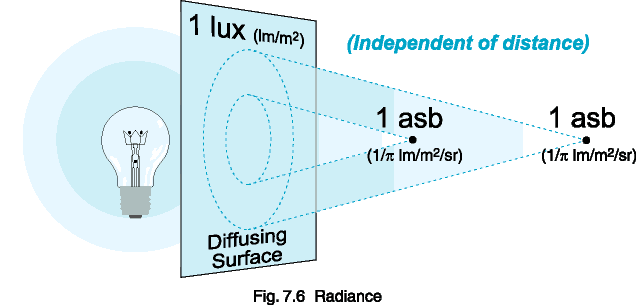 Radiance is a measure of the flux density per unit solid viewing angle,
expressed in W/cm2/sr. Radiance is independent of distance
for an extended area source, because the sampled area increases with distance,
cancelling inverse square losses.
Radiance is a measure of the flux density per unit solid viewing angle,
expressed in W/cm2/sr. Radiance is independent of distance
for an extended area source, because the sampled area increases with distance,
cancelling inverse square losses.
The radiance, L, of a diffuse (Lambertian) surface is related to the
radiant exitance (flux density), M, of a surface by the relationship:
L = M / p
Some luminance units (apostilbs, lamberts, and foot-lamberts) already
contain p in the denominator, allowing simpler
conversion to illuminance units.
Example:
Suppose a diffuse surface with a reflectivity, r,
of 85% is exposed to an illuminance, E, of 100.0 lux (lm/m2)
at the plane of the surface. What would be the luminance, L, of that
surface, in cd/m2?
Solution:
1.) Calculate the luminous exitance of the surface:
M = E * rM = 100.0 * 0.85 =
85.0 lm/m2
2.) Calculate the luminance of the surface:
L = M / p
L = 85.0 / p = 27.1 lm/m2/sr
= 27.1 cd/m2
Irradiance From An Extended Source:
The irradiance, E, at any distance from a uniform extended area source,
is related to the radiance, L, of the source by the following relationship,
which depends only on the subtended central viewing angle, q,
of the radiance detector:
E = p L sin2(q/2)
So, for an extended source with a radiance of 1 W/cm2/sr,
and a detector with a viewing angle of 3°, the irradiance at any distance
would be 2.15 x 10-3 W/cm2. This assumes, of
course, that the source extends beyond the viewing angle of the detector
input optics.
Units Conversion: Radiance & Luminance
RADIANCE:
1 W/cm2/sr (watts per sq. cm per steradian)
= 6.83 x 106 lm/m2/sr at 555 nm
= 683 cd/cm2 at 555 nm
LUMINANCE:
1 lm/m2/sr (lumens per sq. cm per steradian)
= 1 candela/m2 (cd/m2)
= 1 nit
= 10-4 lm/cm2/sr
= 10-4 cd/cm2
= 10-4 stilb (sb)
= 9.290 x 10-2 cd/ft2
= 9.290 x 10-2 lm/ft2/sr
= p apostilbs (asb)
= p cd/p/m2
= p x 10-4 lamberts (L)
= p x 10-4 cd /p/cm2
= 2.919 x 10-1 foot-lamberts (fL)
= 2.919 x 10-1 lm/p/ft2/sr
Radiant and Luminous Intensity:
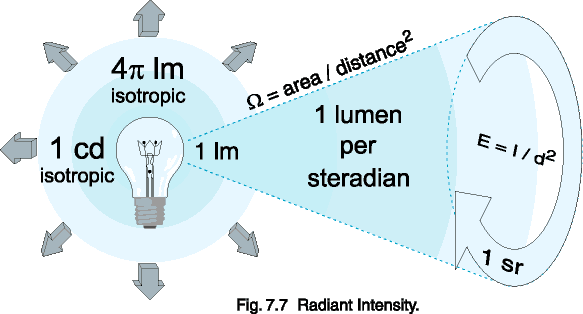 Radiant Intensity is a measure of radiometric power per unit solid angle,
expressed in watts per steradian. Similarly, luminous intensity is
a measure of visible power per solid angle, expressed in candela (lumens
per steradian). Intensity is related to irradiance by the inverse
square law, shown below in an alternate form:
I = E * d2
Radiant Intensity is a measure of radiometric power per unit solid angle,
expressed in watts per steradian. Similarly, luminous intensity is
a measure of visible power per solid angle, expressed in candela (lumens
per steradian). Intensity is related to irradiance by the inverse
square law, shown below in an alternate form:
I = E * d2
If you are wondering how the units cancel to get flux/sr from flux/area
times distance squared, remember that steradians are a dimensionless quantity.
The solid angle equals the area divided by the square of the radius, so
d2=A/W, and substitution yields:
I = E * A / W
The biggest source of confusion regarding intensity measurements involves
the difference between Mean Spherical Candela and Beam Candela, both of
which use the candela unit (lumens per steradian). Mean spherical
measurements are made in an integrating sphere, and represent the total
output in lumens divided by 4p sr in a sphere.
Thus, a one candela isotropic lamp produces one lumen per steradian.
 Beam candela, on the other hand, samples a very narrow angle and is only
representative of the lumens per steradian at the peak intensity of the
beam. This measurement is frequently misleading, since the sampling
angle need not be defined.
Beam candela, on the other hand, samples a very narrow angle and is only
representative of the lumens per steradian at the peak intensity of the
beam. This measurement is frequently misleading, since the sampling
angle need not be defined.
Suppose that two LEDís each emit 0.1 lm total in a narrow beam: One
has a 10° solid angle and the other a 5° angle. The
10° LED has an intensity of 4.2 cd, and the 5° LED an intensity
of 16.7 cd. They both output the same total amount of light, however
-- 0.1 lm.
A flashlight with a million candela beam sounds very bright, but if
its beam is only as wide as a laser beam, then it wonít be of much use.
Be wary of specifications given in beam candela, because they often misrepresent
the total output power of a lamp.
Units Conversion: Intensity
RADIANT INTENSITY:
1 W/sr (watts per steradian)
= 12.566 watts (isotropic)
= 4*p W
= 683 candela at 555 nm
LUMINOUS INTENSITY:
1 lm/sr (lumens per steradian)
= 1 candela (cd)
= 4*p lumens (isotropic)
= 1.464 x 10-3 watts/sr at 555 nm
Converting Between Geometries
Converting between geometry-based measurement units is difficult, and should
only be attempted when it is impossible to measure in the actual desired
units. You must be aware of what each of the measurement geometries
implicitly assumes before you can convert. The example below shows
the conversion between lux (lumens per square meter) and lumens.
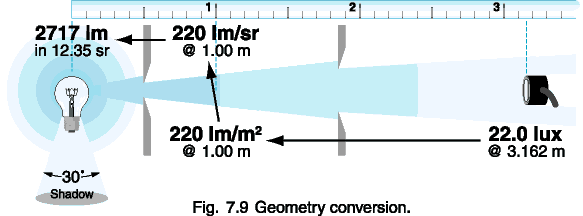
Example:
You measure 22.0 lux from a light bulb at a distance of 3.162 meters.
How much light, in lumens, is the bulb producing? Assume that the
clear enveloped lamp is an isotropic point source, with the exception that
the base blocks a 30° solid angle.
Solution:
1.) Calculate the irradiance at 1.0 meter:
E1 = (d2 / d1)2 * E2
E1.0 m = (3.162 / 1.0)2 * 22.0 = 220 lm/m2
2.) Convert from lm/m2 to lm/sr at 1.0 m:
220 lm/m2 * 1 m2/sr = 220 lm/sr
3.) Calculate the solid angle of the lamp:
W = A / r2 = 2ph
/ r = 2p[1 - cos(a
/ 2)]
W = 2p[1 - cos(330
/ 2)] = 12.35 sr
4.) Calculate the total lumen output:
220 lm/sr * 12.35 sr = 2717 lm

 HOME
Copyright © 1997
International Light, Inc.
Alex
Ryer 26.September.1997
HOME
Copyright © 1997
International Light, Inc.
Alex
Ryer 26.September.1997
 Measurement
Geometries
Measurement
Geometries Measurement
Geometries
Measurement
Geometries








