

Next: Velocity moments
Up: CVonline
Previous: CVonline
Orthogonal Complex Zernike Moments
Complex Zernike moments [5] are constructed using a set of complex polynomials which form a complete orthogonal
basis set defined on the unit disc
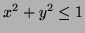 . They are expressed as:
. They are expressed as:
![\begin{displaymath}
A_{mn} = \frac{m+1}{\pi} \int \int_{x^{2} + y^{2} \leq ~1} f(x,y)[V_{mn}(x,y)]^{*} ~dx~dy
\end{displaymath}](img2.png) |
(1) |
where
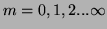 ,
, 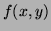 is the function being described,
is the function being described,  denotes the complex conjugate and
denotes the complex conjugate and 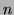 is an
integer, subject to the conditions:
is an
integer, subject to the conditions:
 |
(2) |
The Zernike polynomials [2] 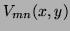 , expressed in polar coordinates are:
, expressed in polar coordinates are:
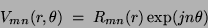 |
(3) |
where 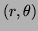 are defined over the unit disc and
are defined over the unit disc and
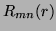 is the orthogonal radial polynomial, defined as:
is the orthogonal radial polynomial, defined as:
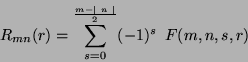 |
(4) |
where:
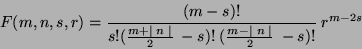 |
(5) |
The first six orthogonal radial polynomials are:
Figure 1 shows eight such radial responses, where it can been seen that the polynomials become more grouped, as they approach the edge of the unit disc.
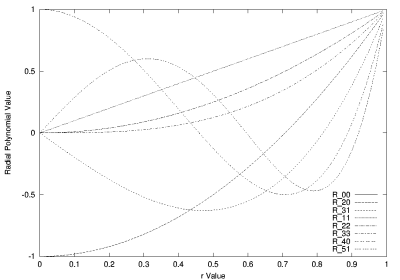 |
Figure 1:
Eight orthogonal radial polynomial plots.
|
|
So for a discrete image, if 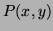 is the current pixel then Equation 1 becomes :
is the current pixel then Equation 1 becomes :
![\begin{displaymath}
A_{mn} = \frac{m+1}{\pi} \sum_{x} \sum_{y} P(x,y)[V_{mn}(x,y)]^{*} ~~~~~\mbox{where $x^{2} + y^{2} \leq ~1$}
\end{displaymath}](img22.png) |
(7) |
To calculate the Zernike moments of an image 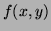 , the image (or region of interest) is first mapped to the unit disc using polar coordinates, where the centre of the image is the origin of the unit disc.
Those pixels falling outside the unit disc are not used in the calculation.
The coordinates are then described by
, the image (or region of interest) is first mapped to the unit disc using polar coordinates, where the centre of the image is the origin of the unit disc.
Those pixels falling outside the unit disc are not used in the calculation.
The coordinates are then described by  which is the length of the vector from the origin to the coordinate point and
which is the length of the vector from the origin to the coordinate point and 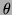 which is the angle from the
which is the angle from the 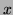 axis to the vector
axis to the vector  , by convention measured from the positive
, by convention measured from the positive 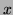 axis in a counter clockwise direction.
The mapping from Cartesian to polar coordinates is:
axis in a counter clockwise direction.
The mapping from Cartesian to polar coordinates is:
 |
(8) |
where
 |
(9) |
However, 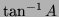 in practice is often defined over the interval
in practice is often defined over the interval
 , so care must be taken as to which quadrant the Cartesian coordinates appear in.
Translation and scale invariance can be achieved by normalising the image using the Cartesian moments prior to calculation of the Zernike moments [1].
Translation invariance is achieved by moving the origin to the centre of the image by using the centralised moments, causing
, so care must be taken as to which quadrant the Cartesian coordinates appear in.
Translation and scale invariance can be achieved by normalising the image using the Cartesian moments prior to calculation of the Zernike moments [1].
Translation invariance is achieved by moving the origin to the centre of the image by using the centralised moments, causing
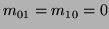 . Following this, scale invariance is produced by altering each object so that its area (or pixel count for a binary image) is
. Following this, scale invariance is produced by altering each object so that its area (or pixel count for a binary image) is  , where
, where 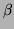 is a predetermined value. Both invariance properties can be achieved using :
is a predetermined value. Both invariance properties can be achieved using :
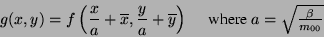 |
(10) |
and  is the new translated and scaled function.
The error involved in the discrete implementation can be reduced by interpolation. If the coordinate calculated by Equation 10 does not coincide with an actual grid location, the pixel value associated with it is interpolated from the four surrounding pixels.
As a result of the normalisation, the Zernike moments
is the new translated and scaled function.
The error involved in the discrete implementation can be reduced by interpolation. If the coordinate calculated by Equation 10 does not coincide with an actual grid location, the pixel value associated with it is interpolated from the four surrounding pixels.
As a result of the normalisation, the Zernike moments
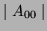 and
and
 are set to known values.
are set to known values.
 is set to zero, due to the translation of the shape to the centre of the coordinate system. This however will be affected by a discrete implementation where the error will decrease as the image size increases.
is set to zero, due to the translation of the shape to the centre of the coordinate system. This however will be affected by a discrete implementation where the error will decrease as the image size increases.
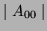 is dependent on
is dependent on  , and thus on
, and thus on 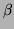 :
:
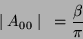 |
(11) |
Further, the absolute value of a Zernike moment is rotation invariant as reflected in the mapping of the image to the unit disc.
The rotation of the shape around the unit disc is expressed as a phase change, if 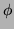 is the angle of rotation,
is the angle of rotation,
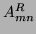 is the Zernike moment of the rotated image and
is the Zernike moment of the rotated image and  is the Zernike moment of the original image then:
is the Zernike moment of the original image then:
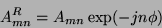 |
(12) |


Next: Velocity moments
Up: CVonline
Previous: CVonline
Jamie Shutler
2001-09-25
![]() . They are expressed as:
. They are expressed as:
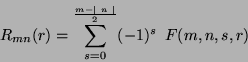
![\begin{displaymath}
A_{mn} = \frac{m+1}{\pi} \sum_{x} \sum_{y} P(x,y)[V_{mn}(x,y)]^{*} ~~~~~\mbox{where $x^{2} + y^{2} \leq ~1$}
\end{displaymath}](img22.png)