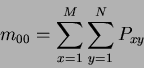

Next: Centralised moments
Up: Non-orthogonal moments
Previous: Non-orthogonal moments
Cartesian moments
The discrete version of the Cartesian moment (Equation 1.13) for an image consisting of pixels
 , replacing the integrals with summations, is:
, replacing the integrals with summations, is:
 |
(16) |
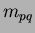 Two dimensional Cartesian moment
Where
Two dimensional Cartesian moment
Where 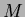 and
and 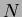 are the image dimensions and the monomial product
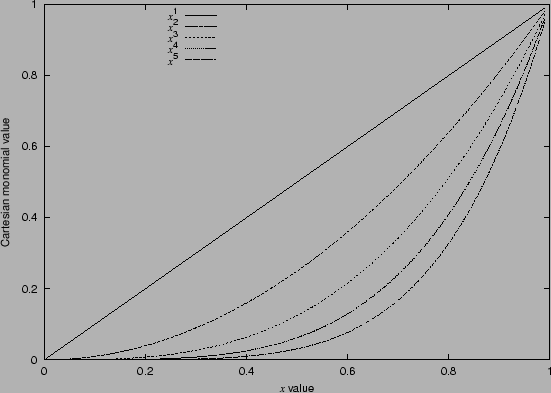
are the image dimensions and the monomial product 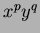 is the basis function. Figure 1.2 illustrates the non-orthogonal (highly correlated) nature of these monomials (in contrast to the orthogonal polynomials in Figure 1.6, to be discussed later) plotted for the positive
is the basis function. Figure 1.2 illustrates the non-orthogonal (highly correlated) nature of these monomials (in contrast to the orthogonal polynomials in Figure 1.6, to be discussed later) plotted for the positive  axis only.
axis only.
Figure 1.2:
The first five Cartesian monomials.
 |
The zero order moment 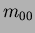 is defined as the total mass (or power) of the image. If this is
applied to a binary (i.e. a silhouette)
is defined as the total mass (or power) of the image. If this is
applied to a binary (i.e. a silhouette) 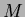

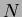 image of an object, then this is literally a
pixel count of the number of pixels comprising the object.
image of an object, then this is literally a
pixel count of the number of pixels comprising the object.
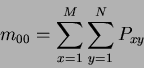 |
(17) |
The two first order moments are used to find the Centre Of Mass (COM)COMCentre of mass of an image. If this is
applied to a binary image and the results are then normalised with respect to the
total mass (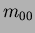 ), then the result is the centre co-ordinates of the object. Accordingly, the centre
co-ordinates
), then the result is the centre co-ordinates of the object. Accordingly, the centre
co-ordinates

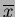
 axis centre of mass
axis centre of mass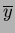
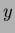 axis centre of mass are given by :
axis centre of mass are given by :
 |
(18) |
The COM describes a unique position within the field of view which can then be used to compute the
centralised moments of an image.


Next: Centralised moments
Up: Non-orthogonal moments
Previous: Non-orthogonal moments
Jamie Shutler
2002-08-15
![]() , replacing the integrals with summations, is:
, replacing the integrals with summations, is: