In the case of perspective cameras, we rewrite (1) for the all views and points as
If all the depth parameters 
are known, we can construct
a 
measurement matrix 
and decompose it
into camera motion 
and object shape 
using
SVD in a similar manner as affine cases. This factorization has the
following ambiguity; Let 
be the projective depths which
give a measurement matrix that can be decomposed into motion and shape
as in (10). Then the following
equation holds for any 4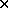
4 non-singular matrix 
and any non-zero scalars 
and
:
where
From these two equations, we can observe two things:
} yields a measurement matrix that can be
decomposed into motion and shape, another family
{
} given by (11)
also yields a decomposable measurement matrix. Therefore,
without loss of generality, we can choose one view, say
i=1, and one object point, say k=1, and fix the depths
associated with this view and this point to unity:
Consequently, the number of independent depth parameters is
.
and
by factoring two
measurement matrices constructed from two depth families
{
} and {
},these two
solutions are then related by using an unknown non-singular
matrix 
and unknown scalars 
and 
as
