Given N observations 
of a random variable X,
the order statistics are obtained by sorting the 
in ascending
order. This produces 
satisfying:
The 
are the order statistics of the N observations
[8].
An Order Statistic Filter (OSF) is a estimator
of the mean
of X which uses a linear combination of order statistics:
Order Statistic Filters have long been known to statisticians
as 
-estimators, but were re-christened and applied to image
processing problems by Bovik et. al. [6].
Some common filters which fit the order statistic filter framework are:
For image processing applications, N is almost always odd, so the question of how to handle even values of N is avoided.
For any distribution, one can determine the optimal coefficients
by minimizing the criterion function
where 
is the vector of order statistic filter
coefficients, 
is the vector of order statistics, and
is the mean of the random variable X. It turns out
that the linear average is optimal for the Gaussian distribution.
Table 1.1 gives OSF coefficients for Gaussian,
Laplacian and Uniform noise, for the case N=9. Bovik
[6] lists optimal coefficients for several other
distributions.
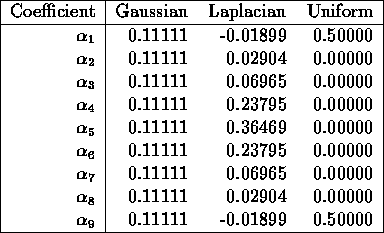
Table 1.1: OSF filter coefficients for N=9
An aspect of order statistic filters which turns out to be
important for Grid Filters is that they
are piecewise linear. The filter partitions 
into N! regions of the form
where 
is a permutation of
. Over each of these regions, the filter output
is a linear function (1.9).
Figure 1.3: Effect of local averages and median filters on fine details
To apply an order statistic filter to an image, one typically
uses 3x3, 5x5 or 7x7 windows.
For non-Gaussian noise, the optimal OSF is superior to taking
a local average for flat regions.
The main problem with such filters is the
underlying stationarity assumption: the derivation of
the OSF assumes that X is a stationary point process,
an assumption which is grossly violated if there is an
edge, line, or other strong signal activity in the window.
Figure 1.3 illustrates this for a test image degraded
by additive white Gaussian noise with 
.
The median filter (lower left) preserves
edges (the checkerboard and the bagel), but wipes out
fine details (the text and lines). The 3x3 average, which
is the optimal OSF for Gaussian noise, blurs too much.
These limitations motivated the development of the Adaptive
Trimmed Mean Filter [9], which makes the assumption
that the signal is smoothly varying within the local window.
When the signal varies slowly within the window, the filter
behaves like a trimmed mean. When an abrupt transition is
detected, the filter behaves like a median, which preserves
edges. Unfortunately, the median filter also destroys fine
details, as illustrated in Figure 1.3.
Another extension of OSFs to the nonstationary case, called a Permutation
Filter or or 
-filter
[10], has
apparently not yet been tested on image restoration problems.
