



Next: Learning Deformable Templates
Up: Prototype-based Parametric Deformable
Previous: Prototype-based Parametric Deformable
We now briefly describe a particular implementation of a prototype-based
model for object matching which has been used in a number of applications
including image database retrieval and object tracking in image sequences
[20,41,47,46].
To encode both the prior shape information and the given shape instance, the deformable template model
is constructed which includes:
(i) a prototype template which describes a representative shape
of a class of objects in terms of a bitmap sketch, (ii) a set of
parametric transformations which deform the template, and (iii) a
probability distribution defined on the set of deformation mappings which
biases the choice of possible deformed templates.
The prototype is represented by a bitmap sketch which
describes the representative shape/boundary
of a class of objects.
Such a scheme captures the global structure of a shape without specifying a parametric form for each class of shapes.
To obtain a shape instance, we apply to the prototype
a transformation characterized by a set of deformation parameter
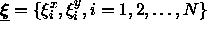 ,
where
,
where 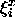 and
and  's are the coefficients of the prespecified deformation basis functions
which span the deviation of the deformed template
from the prototype, and N is the number of deformation basis parameters.
Figure 2 shows an example
of deforming a handrawn bird template using a two-dimensional trigonometric basis.
's are the coefficients of the prespecified deformation basis functions
which span the deviation of the deformed template
from the prototype, and N is the number of deformation basis parameters.
Figure 2 shows an example
of deforming a handrawn bird template using a two-dimensional trigonometric basis.

Figure 2: Deformation of a bird template using a 2D trigonometric basis.
An i.i.d. zero-mean Gaussian distribution is imposed on the
deformation parameters so that the prototype will be most like the
object shape; the larger the deformation, the less likely the deformed template will be generated.
The prototype  , together with the deformation basis and the probability distribution of the deformation coefficients determines the structure of the shape class
and the way the template deforms. The Bayesian prior
for the deformable template
, together with the deformation basis and the probability distribution of the deformation coefficients determines the structure of the shape class
and the way the template deforms. The Bayesian prior
for the deformable template 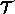 is:
is:
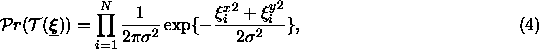
where 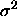 is the variance of the parameters.
is the variance of the parameters.
The deformable template 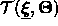 with deformation parameter
with deformation parameter 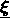 and
pose parameter
and
pose parameter 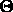 (position, orientation, scale) interacts with an input image I via an
external energy term (or image energy term)
(position, orientation, scale) interacts with an input image I via an
external energy term (or image energy term)
 which measures the agreement between the template
which measures the agreement between the template  and the image I.
The image energy term is specified based on the application requirements,
and the available information. In [20], an image potential energy
which combines both the edge position and the edge tangent information
was used:
and the image I.
The image energy term is specified based on the application requirements,
and the available information. In [20], an image potential energy
which combines both the edge position and the edge tangent information
was used:

where 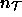 is the number of pixels on the template,
is the number of pixels on the template,
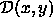 is the distance of the template pixel
is the distance of the template pixel 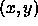 to its
nearest image edge pixel
to its
nearest image edge pixel 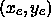 and
and
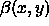 is the angle between the tangent of the nearest edge and the
tangent direction of the template at
is the angle between the tangent of the nearest edge and the
tangent direction of the template at 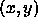 .
The summation is over all the pixels on the deformed template.
This potential energy is designed
so that the template
.
The summation is over all the pixels on the deformed template.
This potential energy is designed
so that the template 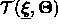 possesses a low potential
possesses a low potential 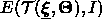 when it
agrees with the input image edge pixels in both position and local
orientation. A Gibbs distribution based on the edge potential
can be used as the likelihood function, which specifies the probability
of observing the input image, given a deformed template at a configuration:
when it
agrees with the input image edge pixels in both position and local
orientation. A Gibbs distribution based on the edge potential
can be used as the likelihood function, which specifies the probability
of observing the input image, given a deformed template at a configuration:

where 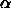 is a normalizing constant to ensure that the above function integrates to 1.
is a normalizing constant to ensure that the above function integrates to 1.
To maximize the posteriori probability derived from the above mentioned
prior and likelihood is equivalent to minimize the following term:

The above function is minimized w.r.t. the deformation parameters 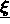 and
pose parameters
and
pose parameters 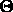 . The first term penalizes the deviation from the prototype.
The second term,
. The first term penalizes the deviation from the prototype.
The second term,
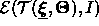 ,
measures the likelihood of the image given the template.
The resulting objective function value is thresholded to decide whether the desired object shape is present in the image.
A coarse-to-fine
implementation of the matching algorithm is used to automatically search an input image for a specified shape irrespective of its position and orientation.
Only moderate scale changes can be accommodated.
An example where the template consists of an open curve
is shown in Fig. 3.
Despite the different appearances of the hands in the input images,
we can correctly localize all of them using the same template.
,
measures the likelihood of the image given the template.
The resulting objective function value is thresholded to decide whether the desired object shape is present in the image.
A coarse-to-fine
implementation of the matching algorithm is used to automatically search an input image for a specified shape irrespective of its position and orientation.
Only moderate scale changes can be accommodated.
An example where the template consists of an open curve
is shown in Fig. 3.
Despite the different appearances of the hands in the input images,
we can correctly localize all of them using the same template.

Figure 3: Automatic localization of human hand using coarse-to-fine algorithm.
(a) the hand template;
(b) input images 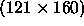 which contain a hand;
(c) retrieved hands overlaid on the input image.
which contain a hand;
(c) retrieved hands overlaid on the input image.




Next: Learning Deformable Templates
Up: Prototype-based Parametric Deformable
Previous: Prototype-based Parametric Deformable
Bob Fisher
Wed May 5 18:16:24 BST 1999
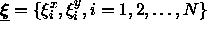 ,
where
,
where 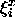 and
and  's are the coefficients of the prespecified deformation basis functions
which span the deviation of the deformed template
from the prototype, and N is the number of deformation basis parameters.
Figure 2 shows an example
of deforming a handrawn bird template using a two-dimensional trigonometric basis.
's are the coefficients of the prespecified deformation basis functions
which span the deviation of the deformed template
from the prototype, and N is the number of deformation basis parameters.
Figure 2 shows an example
of deforming a handrawn bird template using a two-dimensional trigonometric basis.





 , together with the deformation basis and the probability distribution of the deformation coefficients determines the structure of the shape class
and the way the template deforms. The Bayesian prior
for the deformable template
, together with the deformation basis and the probability distribution of the deformation coefficients determines the structure of the shape class
and the way the template deforms. The Bayesian prior
for the deformable template 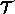 is:
is:
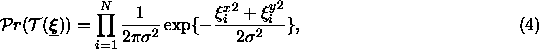
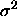 is the variance of the parameters.
is the variance of the parameters.
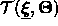 with deformation parameter
with deformation parameter 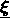 and
pose parameter
and
pose parameter 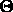 (position, orientation, scale) interacts with an input image I via an
external energy term (or image energy term)
(position, orientation, scale) interacts with an input image I via an
external energy term (or image energy term)
 which measures the agreement between the template
which measures the agreement between the template  and the image I.
The image energy term is specified based on the application requirements,
and the available information. In [
and the image I.
The image energy term is specified based on the application requirements,
and the available information. In [
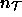 is the number of pixels on the template,
is the number of pixels on the template,
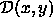 is the distance of the template pixel
is the distance of the template pixel 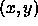 to its
nearest image edge pixel
to its
nearest image edge pixel 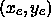 and
and
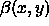 is the angle between the tangent of the nearest edge and the
tangent direction of the template at
is the angle between the tangent of the nearest edge and the
tangent direction of the template at 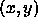 .
The summation is over all the pixels on the deformed template.
This potential energy is designed
so that the template
.
The summation is over all the pixels on the deformed template.
This potential energy is designed
so that the template 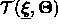 possesses a low potential
possesses a low potential 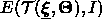 when it
agrees with the input image edge pixels in both position and local
orientation. A Gibbs distribution based on the edge potential
can be used as the likelihood function, which specifies the probability
of observing the input image, given a deformed template at a configuration:
when it
agrees with the input image edge pixels in both position and local
orientation. A Gibbs distribution based on the edge potential
can be used as the likelihood function, which specifies the probability
of observing the input image, given a deformed template at a configuration:

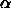 is a normalizing constant to ensure that the above function integrates to 1.
is a normalizing constant to ensure that the above function integrates to 1.

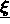 and
pose parameters
and
pose parameters 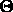 . The first term penalizes the deviation from the prototype.
The second term,
. The first term penalizes the deviation from the prototype.
The second term,
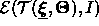 ,
measures the likelihood of the image given the template.
The resulting objective function value is thresholded to decide whether the desired object shape is present in the image.
A coarse-to-fine
implementation of the matching algorithm is used to automatically search an input image for a specified shape irrespective of its position and orientation.
Only moderate scale changes can be accommodated.
An example where the template consists of an open curve
is shown in Fig.
,
measures the likelihood of the image given the template.
The resulting objective function value is thresholded to decide whether the desired object shape is present in the image.
A coarse-to-fine
implementation of the matching algorithm is used to automatically search an input image for a specified shape irrespective of its position and orientation.
Only moderate scale changes can be accommodated.
An example where the template consists of an open curve
is shown in Fig. 
 which contain a hand;
(c) retrieved hands overlaid on the input image.
which contain a hand;
(c) retrieved hands overlaid on the input image.