Perspective projection into two views

  Let $\cal C$, $\cal C'$, be two cameras, with respective optical centers C,C', we associate the frame ${\cal R}_c$ of ${\cal P}^3$to the camera $\cal C$ and the frame ${\cal R}_{c'}$ of ${\cal P}^3$to the camera $\cal C'$.

Let M be a point of the projective space ${\cal P}^3$, represented in ${\cal R}_c$ by $M_{/{\cal R}_c}=(X_c,Y_c,Z_c,T_c)^t$ and in ${\cal R}_{c'}$ by $M_{/{\cal R}_{c'}}=(X_{c'},Y_{c'},Z_{c'},T_{c'})^t$, we call m and m' their two respective projections in the frame induced by ${\cal R}_c$ in the focal plane of the camera $\cal C$, and by ${\cal R}_{c'}$ in the focal plane of the camera $\cal C'$.

the relation (1) can be written for the point m':

 

$$Z_{c'}m' = A'P_0M_{/{\cal R}_{c'}}$$ (6)

we have also:  

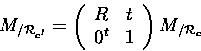$$M_{/{\cal R}_{c'}} = \left ( \begin {array}{c c} R & t\ 0^t & 1\ \end{array} \right) M_{/{\cal R}_{c}}$$ (7)

combining (6) and (7) and doing some calculus we obtain the relation 8:

 

$$Z_{c'}m' = Z_c H_{\infty}m + T_cA't$$ (8)

where  

$$H_{\infty} = A' R A^{-1}$$ (9)

$H_{\infty}$ is the homography of the infinite plane. Note that if t=0 (i.e. we have no translation between the two views, but only rotation), the relation 9 will become a homographic relation (i.e. relation in the projective plane ${\cal P}^2$).

Obviously, if the points are coplanar we have also a homographic relation between the points. In formula 10 we present the relation in case of co-planarity (we obtain this relation starting from formula 8 and doing some simplification using the co-planarity of the points).

 

Z_c'm' = Z_c H m

where:

$$H = H_{\infty} + \frac{1}{d}e'n^tA^{-1}$$ (11)