Classification includes a broad range of decision-theoretic approaches to the identification of images (or parts thereof). All classification algorithms are based on the assumption that the image in question depicts one or more features (e.g., geometric parts in the case of a manufacturing classification system, or spectral regions in the case of remote sensing, as shown in the examples below) and that each of these features belongs to one of several distinct and exclusive classes. The classes may be specified a priori by an analyst (as in supervised classification) or automatically clustered (i.e. as in unsupervised classification) into sets of prototype classes, where the analyst merely specifies the number of desired categories. (Classification and segmentation have closely related objectives, as the former is another form of component labeling that can result in segmentation of various features in a scene.)
Image classification analyzes the numerical properties of various image features and organizes data into categories. Classification algorithms typically employ two phases of processing: training and testing. In the initial training phase, characteristic properties of typical image features are isolated and, based on these, a unique description of each classification category, i.e. training class, is created. In the subsequent testing phase, these feature-space partitions are used to classify image features.
The description of training classes is an extremely important component of the classification process. In supervised classification, statistical processes (i.e. based on an a priori knowledge of probability distribution functions) or distribution-free processes can be used to extract class descriptors. Unsupervised classification relies on clustering algorithms to automatically segment the training data into prototype classes. In either case, the motivating criteria for constructing training classes is that they are:
A convenient way of building a parametric description of this sort is
via a feature vector 
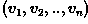, where
n is the number of attributes which describe each image
feature and training class. This representation allows us to consider
each image feature as occupying a point, and each training class as
occupying a sub-space (i.e. a representative point surrounded by some
spread, or deviation), within the n-dimensional
classification space. Viewed as such, the classification problem is
that of determining to which sub-space class each feature
vector belongs.
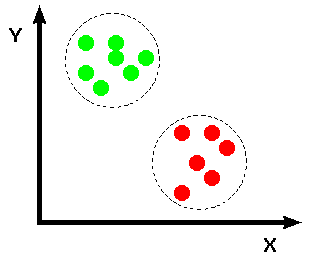
For example, consider an application where we must distinguish two different types of objects (e.g. bolts and sewing needles) based upon a set of two attribute classes (e.g. length along the major axis and head diameter). If we assume that we have a vision system capable of extracting these features from a set of training images, we can plot the result in the 2-D feature space, shown in Figure 1.
Figure 1 Feature space: + sewing needles, o bolts.
At this point, we must decide how to numerically partition the feature space so that if we are given the feature vector of a test object, we can determine, quantitatively, to which of the two classes it belongs. One of the most simple (although not the most computationally efficient) techniques is to employ a supervised, distribution-free approach known as the minimum (mean) distance classifier. This technique is described below.
Minimum (Mean) Distance Classifier
Suppose that each training class is represented by a prototype (or mean) vector:
where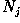 
is the number of training pattern vectors from
class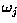 
. In the example classification problem
given above,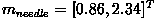 
and
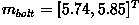as shown in Figure 2.
Figure 2 Feature space: + sewing needles, o bolts, * class mean
Based on this, we can assign any given pattern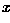 
to the
class of its closest prototype by determining its proximity to each
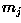. If Euclidean distance is our measure of proximity, then the distance to the prototype is given by
It is not difficult to show that this is equivalent to computing
and assign 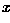to class 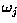if
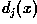yields the largest value.
Returning to our example, we can calculate the following decision functions:
Finally, the decision boundary which separates class
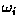from 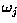is given by
values for 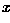for which
In the case of the needles and bolts problem, the decision surface is given by:
As shown in Figure 3, the surface defined by this decision
boundary is the perpendicular bisector of the line segment joining
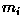and .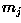
Figure 3 Feature space: + sewing needles, o bolts, * class mean, line = decision surface
In practice, the minimum (mean) distance classifier works well when
the distance between means is large compared to the spread (or
randomness) of each class with respect to its mean. It is simple to
implement and is guaranteed to give an error rate within a factor of
two of the ideal error rate, obtainable with the statistical, supervised
Bayes' classifier. The Bayes' classifier is a more informed
algorithm as the frequencies of occurrence of the features of interest
are used to aid the classification process. Without this information
the minimum (mean) distance classifier can yield biased
classifications. This can be best combatted by applying training
patterns at the natural rates at which they arise in the raw training
set.
To illustrate the utility of classification (using the minimum (mean) distance classifier), we will consider a remote sensing application. Here, we have a collection of multi-spectral images (i.e. images containing several bands, where each band represents a single electro-magnetic wavelength or frequency) of the planet Earth collected from a satellite. We wish to classify each image pixel into one of several different classes (e.g. water, city, wheat field, pine forest, cloud, etc.) on the basis of the spectral measurement of that pixel.
Consider a set of images of the globe (centered on America) which describe the visible
and infra-red
spectrums, respectively. From the histograms of the visible band image
and infra-red band image
we can see that it would be very difficult to find a threshold, or decision surface, with which to segment the images into training classes (e.g. spectral classes which correspond to physical phenomena such as cloud, ground, water, etc.). It is often the case that having a higher dimensionality representation of this information (i.e. using one 2-D histogram instead of two 1-D histograms) facilitates segmentation of regions which might overlap when projected onto a single axis, as shown for some hypothetical data in Figure 4.
Figure 4 2-D feature space representation of hypothetical data. (The projection of the data onto the X-axis is equivalent to a 1-D histogram.)
Since the images over America are registered, we can combine them into
a single two-band image and find the decision surface(s) which divides
the data into distinct classification regions in this higher
dimensional representation. To this aim, we use a k-means
algorithm to find the training classes of the 2-D spectral
images. (This algorithm converts an input image into vectors of equal
size (where the size of each vector is determined by the number of
spectral bands in the input image) and then determines the k
prototype mean vectors by minimizing of the sum of the squared
distances from all points in a class to the class center
.)
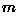If we choose k=2 as a starting point, the algorithm finds two prototype mean vectors, shown with a * symbol in the 2-D histogram
This figure also shows the linear decision surface which separates out our training classes.
Using two training classes, such as those found for the image over America, we can classify a similar multi-spectral image of Africa
(visible) and
(infra-red) to yield the result:
(Note that the image size has been scaled by a factor of two to speed up computation, and a border has been placed around the image to mask out any background pixels.) We can see that one of the classes created during the training process contains pixels corresponding to land masses over north and south Africa, whereas the pixels in the other class represent water or clouds.
Classification accuracy using the minimum (mean) distance classifier improves as we increase the number of training classes. The images
and
show the results of the classification procedure using k=4 and k=6 training classes. The equivalent with a color assigned to each class is shown in
and
for k=4 and k=6, respectively. Here we begin to see the classification segmenting out regions which correspond to distinct physical phenomena.
Classification is such a broad ranging field, that a description of all the algorithms could fill several volumes of text. We have already discussed a common supervised algorithm, therefore in this section we will briefly consider a representative unsupervised algorithm. In general, unsupervised clustering techniques are used less frequently, as the computation time required for the algorithm to learn a set of training classes is usually prohibitive. However, in applications where the features (and relationships between features) are not well understood, clustering algorithms can provide a viable means for partitioning a sample space.
A general clustering algorithm is based on a split and merge
technique, as shown in Figure 5. Using a similarity
measure (e.g. the dot product of two vectors, the weighted Euclidean
distance, etc.), the input vectors can be partitioned into subsets,
each of which should be sufficiently distinct. Subsets which do not
meet this criterion are merged. This procedure is repeated on all of
the subsets until no further splitting of subsets occurs or until some
stopping criteria is met.
Figure 5 General clustering algorithm
You can interactively experiment with this operator by clicking here.
------------------------------------ | Petal Length | Petal Width | Class | |--------------+-------------+-------| | 4 | 3 | 1 | |--------------+-------------+-------| | 4.5 | 4 | 1 | |--------------+-------------+-------| | 3 | 4 | 1 | |--------------+-------------+-------| | 6 | 1 | 2 | |--------------+-------------+-------| | 7 | 1.5 | 2 | |--------------+-------------+-------| | 6.5 | 2 | 2 | ------------------------------------
a) Calculate the mean, or prototype, vectors
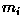for the two flower types described above. b)
Determine the decision functions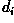 
for each
class. c) Determine the equation of the boundary (i.e.
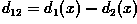) and plot the decision
surface on your graph. d) Notice that substitution of a
pattern from class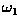 
into your answer from the
previous section yields a positive valued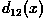 
,
while a pattern belonging to the class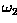 
yields a negative value. How would you use this information to
determine a new pattern's class membership?
and
are the visible and infra-red images of Europe,
and
are those of the United Kingdom and
and
are those of Scandinavia. Begin by combining the two single-band spectral images of Europe into a single multi-band image. (You may want to scale the image so as to cut down the processing time.) Then, create a set of training classes, where k equals 6,8,10... (Remember that although the accuracy of the classification improves with greater numbers of training classes, the computational requirements increase as well.) Then try classifying all three images using these training sets.
T. Avery and G. Berlin Fundamentals of Remote Sensing and Airphoto Interpretation, Maxwell Macmillan International, 1985, Chap. 15.
D. Ballard and C. Brown Computer Vision, Prentice-Hall, Inc., 1982, Chap. 6.
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, Chap. 18.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1986, Chap. 9.
D. Vernon Machine Vision, Prentice-Hall, 1991, Chap. 6.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
