Common Names: Antilogarithm, Exponential Operator, Raise to Power Operator
The exponential and `raise to power' operators are two anamorphosis operators which can be applied to grayscale images. Like the logarithmic transform, they are used to change the dynamic range of an image. However, in contrast to the logarithmic operator, they enhance high intensity pixel values.
The exponential operator is a point process where the mapping function is an exponential curve. This means that each pixel intensity value in the output image is equal to a basis value raised to the value of the corresponding pixel value in the input image. Which basis number is used depends on the desired degree of compression of the dynamic range. In order to enhance the visibility of a normal photograph, values just above 1 are suitable. For display, the image must be scaled such that the maximum value becomes 255 (assuming an 8-bit display). The resulting image is given by
where P and Q are the input and output images, respectively, b is the basis and c is the scaling factor. As we can see from the formula, P=0 yields Q=c. To avoid the resulting offset, many implementations subtract 1 from the exponential term before the scaling. Hence, we get the following formula:
Figure 1 shows the mapping function for b = 10 and b = 1.01.
Figure 1 Exponential mapping functions for(solid line) and b = 1.01, c = 20.2 (dotted line).
We can see from the figure that the curvature of the base 10 exponential function is far too high to enhance the visibility of normal image. We can control the curvature of the mapping function either by choosing the appropriate basis or by scaling down the image prior to applying the exponential operator. This is because, over a low range of input values, an exponential function with a high basis has the same shape as an exponential function with smaller basis over a larger range of input values.
In the case of the `raise to the power' operator, the pixel intensity values in the input image act as the basis which is raised to a (fixed) power. The operator is defined by the following formula:
If r > 1, the `raise to power' operator is similar to the exponential operator in the sense that it increases the bandwidth of the high intensity values at the cost of the low pixel values. However, if r < 1, the process enhances the low intensity value while decreasing the bandwidth of the high intensity values. This is similar to the effect achieved with the logarithmic transform.
Examples for r = 0.5, r=2 and r=6 can be seen in Figure 2.
Figure 2 Mapping function of `raise to power' operator for r=0.5 (dashed line), r = 2 (solid line) and r=6 (dotted line).
The exponential operator is the dual of the logarithmic transform. Hence, one application of the exponential operator is to undo changes originating from the logarithmic operator. In this case, the basis for the exponential operator should be the same as it was for the logarithmic transform. For example,
was obtained from
by applying a base 10 logarithm. If we need to restore the original version, we can do this by replacing each pixel with 10 to the power of its value. However, we have to be careful which image to use as input. If we take the above scaled and quantized image, the result of the exponential operator (after normalizing to the range 0 - 255) is
The reason for this is summarized in the equation below:
where P is the original image, Q1 is the image after the logarithmic transform and Q2 is the final result.
The effect can be seen in the shape of the base 10 exponential function, as shown in Figure 1. To get the original image we need to apply the exponential operator to the unscaled image, containing the values directly after the logarithmic operation, i.e. in this case the log values will all be smaller than 3. If we store the unscaled image in a floating-point format and then apply the exponential operator we obtain the correct original image:
Like the logarithmic operator, the exponential and `raise to power' operators might be used to compress the dynamic range or generally enhance the visibility of an image. Because they can be used to enlarge the range of high intensity pixel values relative to the range of the low intensity values, these operators are suitable for enhancement of images containing details represented by a rather narrow range of high intensity pixel values. For example, in
we might be interested in enhancing the details of the face, because it is slightly over-exposed. Applying an exponential transform with the base 1.005 yields
We can see that the contrast in the high pixel values has been increased at the cost of the contrast in the low pixel values. This effect is magnified if we increase the basis to 1.01. As can be seen in
the resulting image now appears to be too dark.
For comparison,
and
show the original image after a `raise to power' operation with r = 1.5 and r = 2.5, respectively. We can see that both exponential and `raise to power' operator perform similarly at this (rather low) rate of compression. One difference, however, is that the `raise to power' operator does not depend on the scale of the image. The exponential operator, on the other hand, compresses the dynamic range more if the image contains pixels with very high intensity values (e.g. an image in floating point format with high pixel intensity values).
The exponential transform is not always appropriate to enhance the visibility of an image. For example,
is an under-exposed image and we would like to enhance the contrast of the low pixel values. The exponential operator, however, makes the situation even worse, as can be seen in
In this example, the logarithmic operator would be more suitable.
The `raise to power' operator is also known as gamma
correction. In this case, the operator is used to correct for the
non-linear response of a photographic film. The relation between the
exposure of the film E and the resulting intensity value in the
image I can be approximated, over a wide range of E, with the
`raise to power' operator:
where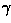 
is called the gamma of the film. A
typical value for gamma lies between 0.7 and 1.0. The gamma
correction usually takes the gamma value as parameter and performs a
`raise to power' transform with r=1/gamma so that the
relation between the initial exposure of the film and the intensity
value in the corrected image becomes linear.
You can interactively experiment with this operator by clicking here.
and
Which of the two images has improved? Try the logarithmic operator for comparison.
What are the effects? Can you see any differences between the two resulting images?
D. Ballard and C. Brown Computer Vision, Prentice-Hall, 1982, p 45.
R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, pp 72, 162 - 163.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1986, pp 232 - 234, 273.
A. Marion An Introduction to Image Processing, Chapman and Hall, 1991, pp 113 - 114.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
