Common Names: Pixel Logarithm, Dynamic Range Compression
The dynamic range of an image can be compressed by replacing each pixel value with its logarithm. This has the effect that low intensity pixel values are enhanced. Applying a pixel logarithm operator to an image can be useful in applications where the dynamic range may too large to be displayed on a screen (or to be recorded on a film in the first place).
The logarithmic operator is a simple point processor where the mapping function is a logarithmic curve. In other words, each pixel value is replaced with its logarithm. Most implementations take either the natural logarithm or the base 10 logarithm. However, the basis does not influence the shape of the logarithmic curve, only the scale of the output values which are scaled for display on an 8-bit system. Hence, the basis does not influence the degree of compression of the dynamic range. The logarithmic mapping function is given by
Since the logarithm is not defined for 0, many implementations of this operator add the value 1 to the image before taking the logarithm. The operator is then defined as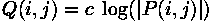
The scaling constant c is chosen so that the maximum output value is 255 (providing an 8-bit format). That means if R is the value with the maximum magnitude in the input image, c is given by
The degree of compression (which is equivalent to the curvature of the mapping function) can be controlled by adjusting the range of the input values. Since the logarithmic function becomes more linear close to the origin, the compression is smaller for an image containing small input values. The mapping function is shown for two different ranges of input values in Figure 1.
Figure 1 Logarithmic mapping functions at two different scales.
The most common application for the dynamic range compression is for the display of the Fourier Transform. We will illustrate this using
The maximum magnitude value of
its Fourier Transform is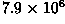 
, and the
second largest value is approximately 10 times smaller. If we
simply linearly scale this image, we obtain
Due to the large dynamic range, we can only recognize the largest value in the center of the image. All remain values appear as black on the screen. If we instead apply the logarithmic operator to the Fourier image, we obtain
Here, smaller pixel values are enhanced and therefore the image shows significantly more details.
The logarithmic operator enhances the low intensity pixel values, while compressing high intensity values into a relatively small pixel range. Hence, if an image contains some important high intensity information, applying the logarithmic operator might lead to loss of information. For example,
is the linearly scaled Fourier Transform of
The image shows one bright spot in the center and two darker spots on the diagonal. We can infer from the image that these three frequencies are the main components of the image with the DC-value having the largest magnitude. Applying the logarithmic transform to the Fourier image yields
Here, we can see that the image contains
many more frequencies. However, it is now hard to tell which are the
dominating ones, since all high magnitudes are compressed into a
rather small pixel value range. The magnitude of compression is large
in this case because there are extremely high intensity values in the
output of the Fourier Transform (in this case up to 
). We
can decrease the compression rate by scaling down the
Fourier image before applying the logarithmic
transform. Image
is the result of first multiplying each pixel with 0.0001 and then taking its logarithm. Now, we can recognize all the main components of the Fourier image and can even see the difference in their intensities.
Thus, a logarithmic transform is appropriate when we want to enhance the low pixel values at the expense of loss of information in the high pixel values. For example, the man in
was photographed in front of a bright background. The dynamic range of the film material is too small, so that the graylevels on the subject's face are clustered in a small pixel value range. A logarithmic transform spreads them over a wider range, while the higher values are compressed. The result can be seen in
On the other hand, applying a logarithmic transform to
is less appropriate, because most of its details are contained in the high pixel values. Applying the logarithmic operator yields
This image shows that a lot of information is lost during the transform.
The logarithmic operator is a member of the family of anamorphosis operators, which are LUT transformations with a strictly increasing or decreasing mapping function.
An anamorphosis operator which is similar to the logarithmic transform is the square-root operator. Its mapping function is defined as
Both operators increase the contrast of low pixel values at the cost of the contrast of high pixel values. Hence, both are suitable to enhance details contained in the low values. However, they produce slightly different enhancements, since the shapes of their curves are not identical.
You can interactively experiment with this operator by clicking here.
Does this process improve the image. What is the reason? What is the result using
R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, pp 167 - 168.
A. Jain Fundamentals of Digital Processing, Prentice Hall, 1989, p 240.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
