






The translate operator performs a geometric transformation which maps
the position of each picture element in an input image into a new
position in an output image, where the dimensionality of the two
images often is, but need not necessarily be, the same. Under
translation, an image element located at 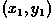 in the
original is shifted to a new position
in the
original is shifted to a new position 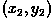 in the
corresponding output image by displacing it through a user-specified
translation
in the
corresponding output image by displacing it through a user-specified
translation 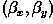 . The treatment of elements near
image edges varies with implementation. Translation is used to improve
visualization of an image, but also has a role as a preprocessor in
applications where registration of two or more images is
required. Translation is a special case of affine
transformation.
. The treatment of elements near
image edges varies with implementation. Translation is used to improve
visualization of an image, but also has a role as a preprocessor in
applications where registration of two or more images is
required. Translation is a special case of affine
transformation.
The translation operator performs a transformation of the form:
Since the dimensions of the input image are well defined, the output
image is also a discrete space of finite dimension. If the new
coordinates 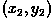 are outside the image, the translate
operator will normally ignore them, although, in some implementations,
it may link the higher coordinate points with the lower ones so as to
wrap the result around back onto the visible space of the image. Most
implementations fill the image areas out of which an image has been
shifted with black pixels.
are outside the image, the translate
operator will normally ignore them, although, in some implementations,
it may link the higher coordinate points with the lower ones so as to
wrap the result around back onto the visible space of the image. Most
implementations fill the image areas out of which an image has been
shifted with black pixels.
The translate operator takes two arguments, 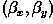 , which specify the desired horizontal and vertical
pixel displacements, respectively. For example, consider the
artificial image
, which specify the desired horizontal and vertical
pixel displacements, respectively. For example, consider the
artificial image
in which the subject's center
lies in the center of the 300×300 pixel image. We can naively
translate the subject into the lower, right corner of the image by
defining a mapping (i.e. a set of values) for 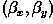 which will take the subject's center from its present
position at
which will take the subject's center from its present
position at 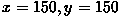 to an output position of
to an output position of
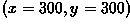 , as shown in
, as shown in
In this case, information is lost because pixels which were mapped to points outside the boundaries defined by the input image were ignored. If we perform the same translation, but wrap the result, all the intensity information is retained, giving image
Both of the mappings shown above disturb the original geometric structure of the scene. It is often the case that we perform translation merely to change the position of a scene object, not its geometric structure. In the above example, we could achieve this effect by translating the circle center to a position located at the lower, right corner of the image less the circle radius
At this point, we might build a collage by adding) another image(s) whose subject(s) has been appropriately translated, such as in
to the previous result. This simple collage is shown in
Translation has many applications of the cosmetic sort illustrated above. However, it is also very commonly used as a preprocessor in application domains where registration of two or more images is required. For example, feature detection and spatial filtering algorithms may calculate gradients in such a way as to introduce an offset in the positions of the pixels in the output image with respect to the corresponding pixels from the input image. In the case of the Laplacian of Gaussian spatial sharpening filter, some implementations require that the filtered image be translated by half the width of the Gaussian kernel with which it was convolved in order to bring it into alignment with the original. Likewise, the unsharp filter, requires translation to achieve a re-registration of images. The result of subtracting the smoothed version of the image
away from the original image (after translating the smoothed image by the offset induced by the filter before we subtract to re-align the two images) yields the edge image
We again view the effects of mis-alignment if we consider translating
by one pixel in the x and y directions and then subtracting this result from the original. The resulting image, shown in
contains a description of all the places (along the direction of translation) where the intensity gradients are different; i.e. it highlights edges (and noise). The image
was used in examples of edge detection using the Roberts Cross, Sobel and Canny operators. Compare this result to the translation-based edge-detector illustrated here
Note that if we increase the translation parameter too much, e.g., by 6 pixels in each direction, as in
edges become severely mis-aligned and blurred.
You can interactively experiment with this operator by clicking here.
into
b)
into
has been translated and then pixel added back onto itself to produce
a) Produce an artificial image of this sort using
b) Combine
and
using translation and pixel addition into a collage.
Figure 1 Convolution kernel.
Can one implement every convolution using this approach?
D. Ballard and C. Brown Computer Vision, Prentice-Hall, 1982, Appendix 1.
B. Horn Robot Vision, MIT Press, 1986, Chap. 3.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.



