





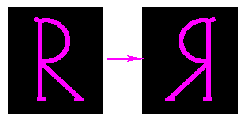
The reflection operator geometrically transforms an image such that
image elements, i.e. pixel values, located at position
 in an original image are reflected about a
user-specified image axis or image point into a new position
in an original image are reflected about a
user-specified image axis or image point into a new position
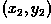 in a corresponding output image. Reflection is
mainly used as an aid to image visualization, but may be used as a
preprocessing operator in much the same way as
rotation. Reflection is a special case of
affine transformation.
in a corresponding output image. Reflection is
mainly used as an aid to image visualization, but may be used as a
preprocessing operator in much the same way as
rotation. Reflection is a special case of
affine transformation.
Reflection can be performed about an image axis or a point in the image. In the case of the former, some commonly used transformations are the following:
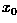 in the input image:
in the input image:
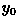 :
:
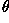 , and passing through
, and passing through 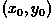 :
:
where 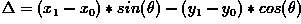 .
.
Note that if 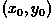 is not in the center of the
input image, part of the image will be reflected out of the visible
range of the image. Most implementations fill in image areas out of
which pixels have been reflected with black pixels.
is not in the center of the
input image, part of the image will be reflected out of the visible
range of the image. Most implementations fill in image areas out of
which pixels have been reflected with black pixels.
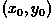 in the input image are given by:
in the input image are given by:
The simplest reflection we can define reflects an image about an axis located in the center of an image. For example, we can reflect
about a vertical axis in the center of the image to produce
Similarly,
shows the reflection of
about a horizontal axis passing through the image center.
Reflection about a point in the center of the image maps
into
This result, of course, could also be achieved by rotating the image through 180 degrees about its center.
A popular application for reflection is  symmetry analysis. For
example, consider the image
symmetry analysis. For
example, consider the image
A quick examination of this face might lead us to believe that the left and right halves were mirror images of each other. However, if we reflect this image (about a carefully selected axis running vertically between the eyes) and then create two new images such that (i) the first contains the original left half of the face, joined in the middle to a reflection of the left half and (ii) the second contains a similar description of the right half of the face, we see that this is not the case. A comparison of the left
and right
reflection images reveals differences in the fur color, eye shape/expression, nose orientation, whisker alignment, etc.
You can interactively experiment with this operator by clicking here.
What sort of reflection might have produced
and
compare the reflection and rotation operators in terms of their computational speed and the quality of the resultant image.
and
Alignment of the axis of reflection with the center of the face is tricky. You might want to consider putting it at a position equi-distant between both eyes.
D. Ballard and C. Brown Computer Vision, Prentice-Hall, 1982, Appendix 1.
B. Horn Robot Vision, MIT Press, 1986, Chap. 3.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.



