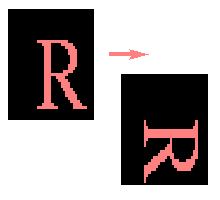
The rotation operator performs a geometric transform which maps the
position 
of a picture element in an input image
onto a position 
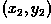in an output image by
rotating it through a user-specified angle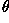 
about
an origin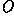 
. In most implementations, output locations
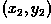which are outside the boundary of the image
are ignored. Rotation is most commonly used to improve the visual
appearance of an image, although it can be useful as a preprocessor
in applications where directional operators are involved. Rotation is
a special case of affine transformation.
The rotation operator performs a transformation of the form:
where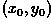 
are the coordinates of the center of
rotation (in the input image) and 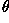is the
angle of rotation with clockwise rotations having positive angles.
(Note here that we are working in image coordinates, so the y axis goes downward.
Similar rotation formula can be defined for when the y axis goes upward.)
Even more than the translate operator, the
rotation operation produces output locations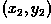
which do not fit within the boundaries of the image (as defined by the
dimensions of the original input image). In such cases, destination
elements which have been mapped outside the image are ignored by most
implementations. Pixel locations out of which an image has been
rotated are usually filled in with black pixels.
The rotation algorithm, unlike that employed by
translation, can produce coordinates
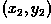which are not integers. In order to generate
the intensity of the pixels at each integer position, different
heuristics (or re-sampling techniques} may be employed. For
example, two common methods include:
.
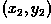The latter method produces better results but increases the computation time of the algorithm.
A rotation is defined by an angle 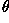and an
origin of rotation 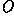. For example, consider the image
whose subject is centered. We can rotate the image
through 180 degrees about the image (and circle) center at
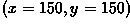to produce
If we use these same parameter settings but a new, smaller image, such as the 222×217 size artificial, black-on-white image
we achieve poor results, as shown in
because the
specified axis of rotation is sufficiently displaced from the image
center that much of the image is swept off the page. Likewise,
rotating this image through a 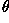value which is not
an integer multiple of 90 degrees (e.g. in this case
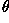equals 45 degrees) rotates part of the image off
the visible output and leaves many empty pixel values, as seen in
(Here, non-integer pixel values were re-sampled using the first technique mentioned above.)
Like translation, rotation may be employed in the early stages of more sophisticated image processing operations. For example, there are numerous directional operators in image processing (e.g. many edge detection and morphological operators) and, in many implementations, these operations are only defined along a limited set of directions: 0, 45, 90, etc. A user may construct a hybrid operator which operates along any desired image orientation direction by first rotating an image through the desired direction, performing the edge detection (or erosion, dilation, etc.), and then rotating the image back to the original orientation. (See Figure 1.)
Figure 1 A variable-direction edge detector.
As an example, consider
whose edges were detected by the directional operator defined using translation giving
We can perform edge detection along the opposite direction to that shown in the image by employing a 180 degree rotation in the edge detection algorithm. The result is shown in
Notice the slight degradation of this image due to rotation re-sampling.
You can interactively experiment with this operator by clicking here.
and
which contain L-shaped parts of different sizes. a) Rotate and translate one of the images such that the bottom left corner of the ``L'' is in the same position in both images. b) Using a combination of histograming, thresholding and pixel arithmetic (e.g. pixel subtraction) determine the approximate difference in size of the two parts.
You should begin by centering the propeller in the middle of the image. Next, rotate the image through a series of 45 degree rotations and add each rotated version back onto the original. (Note: you can improve the visual appearance of the result if you scale the intensity values of each rotated propeller a few shades before adding it onto the collage.)
and
using a 90 degree directional erosion operator. Next, rotate the image through 90 degrees before applying the directional erosion operator along the 0 degree orientation. Compare the results.
D. Ballard and C. Brown Computer Vision, Prentice-Hall, 1982, Appendix 1.
B. Horn Robot Vision, MIT Press, 1986, Chap. 3.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
